Si vous avez survécu au précédent article sur l’Icosaèdre, vous serez alors heureux de savoir que cette première construction va nous servir maintenant à modéliser une balle de golf !

 

 

Modéliser une balle de golf sur Catia V5 !

Mais quel est le rapport entre le solide de Platon et la balle de golf ?

Si vous avez un jour observé attentivement une balle de golf, vous aurez remarqué que les petites cavités ne sont pas disposées selon une simple répétition circulaire comme nous pouvons le voir habituellement sur le net dans les rapides modélisations CAO de pseudo balles de golf.

Non, en vérité, les cavités sont réparties uniformément sur chaque face de l’icosaèdre inscrit dans la sphère de départ.
Vous pouvez aller lire l’article de Wikipédia sur la balle de golf, on y trouve cette représentation issue d’un brevet US.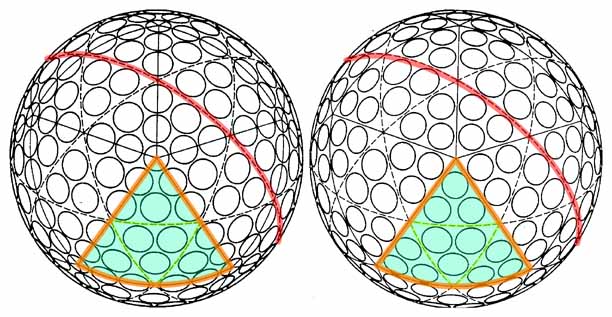

Le grand triangle vert d’eau représente une face de l’icosaèdre.
Je me suis basé sur la représentation de gauche pour construire mon modèle.
Et il me fallait bien un Icosaèdre pour commencer, d’où l’article précédent.

Première étape, une face de l’icosaèdre

Projetons les bords d’une face de l’icosaèdre sur la sphère.
Projection normale, cela donne trois portions de cercle jaune pointillé (qui sont les traces oranges de la représentation de wikipédia).

Deuxième étape positionner des points de position pour les cavités

Il faut ensuite positionner les cavités dans cette surface.

Il suffit pour cela de répartir 4 points sur chaque arête.

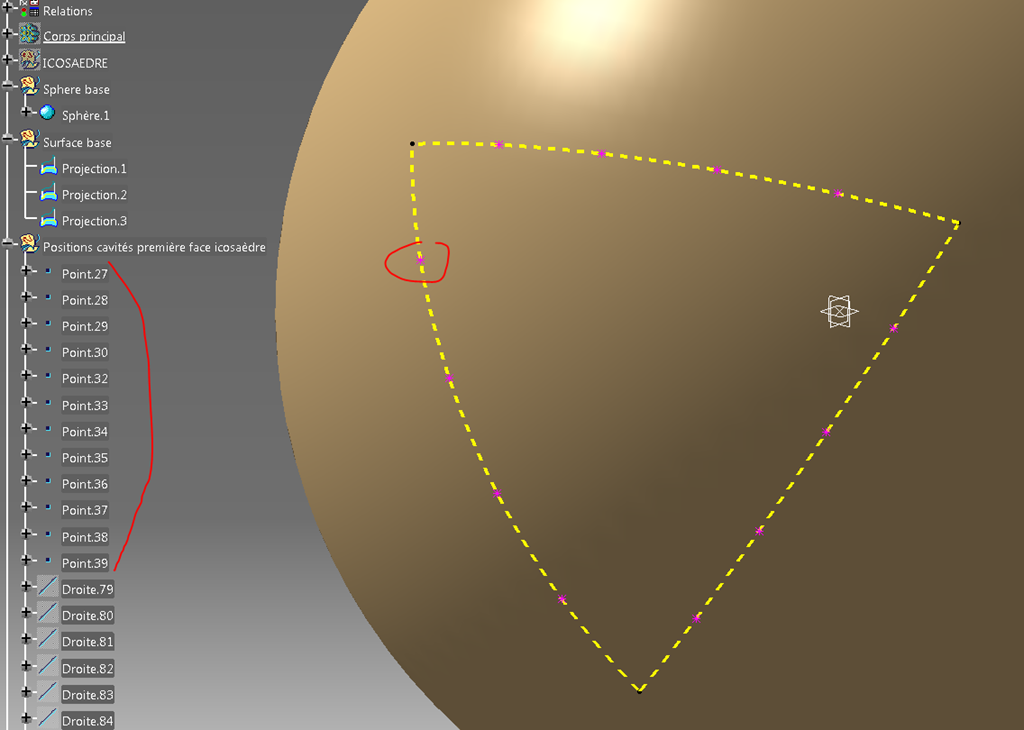
On a alors la position des cavités sur la circonférence de cette face “triangulaire” (portion de sphère).

Il nous faut maintenant les positions à l’intérieur du triangle équilatéral.
C’est facile, il suffit de raccorder par des lignes les points déjà présents comme dans un triangle équilatéral tracé dans un plan.

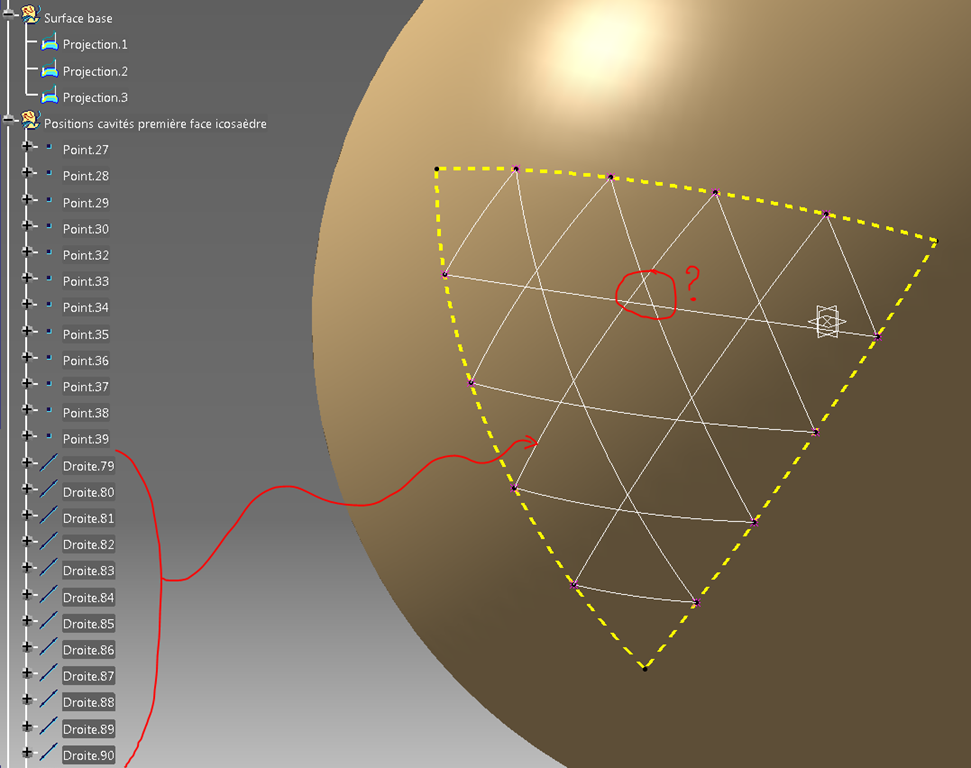
Alors, dans un plan, cela fonctionne parfaitement et les lignes se croisent en un seul point mais ici les projections sur la sphère ne se coupent pas au même endroit.
Je ne sais pas pourquoi et j’ai passé un long moment à trouver en vain une solution, cela conduit toujours à ce résultat.
Si quelqu’un peu m’expliquer le phénomène simplement, je suis preneur.

Pas découragé pour autant, je suis parti du principe que les positions idéales se trouvaient au centre des petits triangles.
J’ai donc fait 6 constructions pour placer un point à ces endroits.

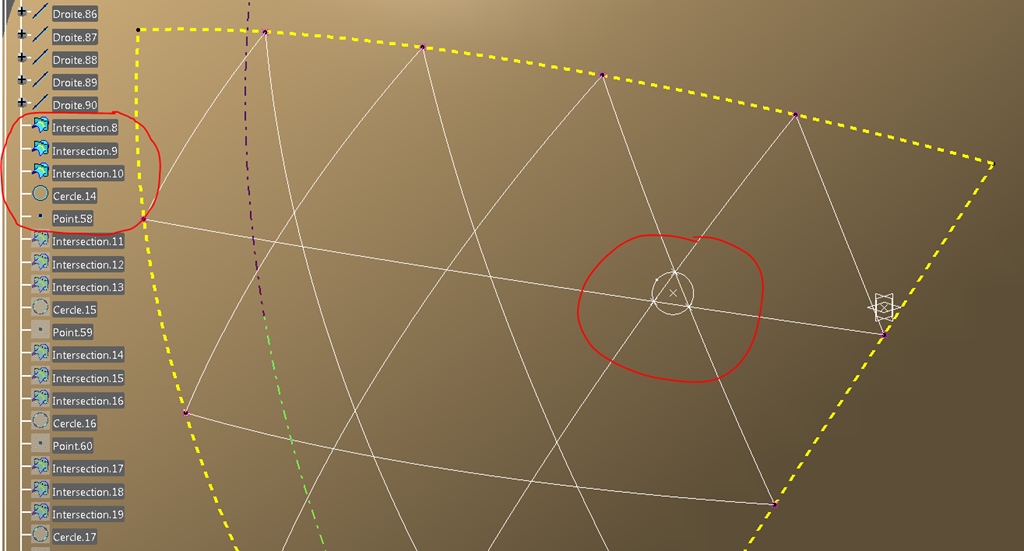
On a ainsi la position de chaque cavité.

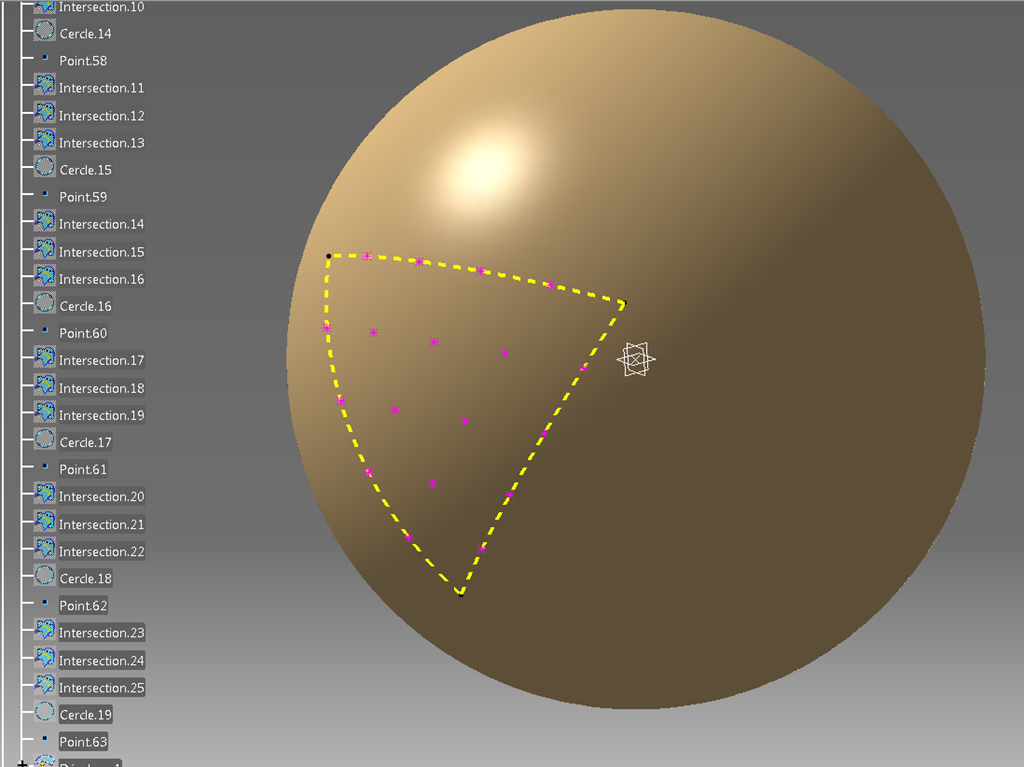
Celles-ci sont ensuite projetées de façon normale sur une sphère décalée.
Cela permet de créer réellement les centres des petites sphères qui représentent les cavités car ces petits creux ne sont pas très profonds (1/4 de sphère tout au plus).

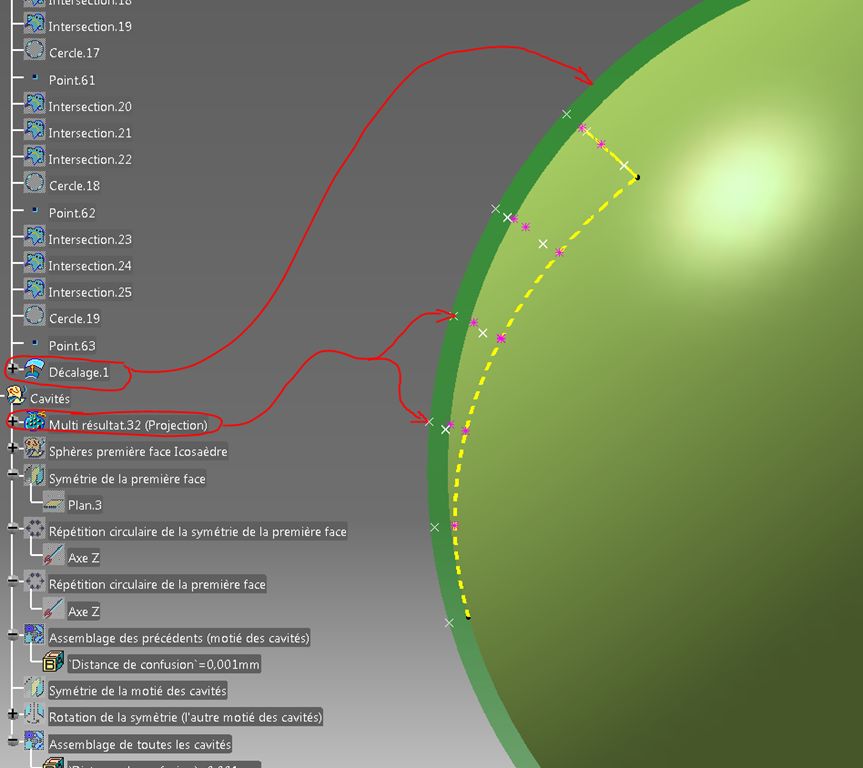
Troisième étape, dessiner les 21 sphères

Là, il suffit de prendre son mal en patience et de s’aider d’un copier/coller.
Un repointage du parent (point de centre) suffit à placer la nouvelle sphère au bon endroit.

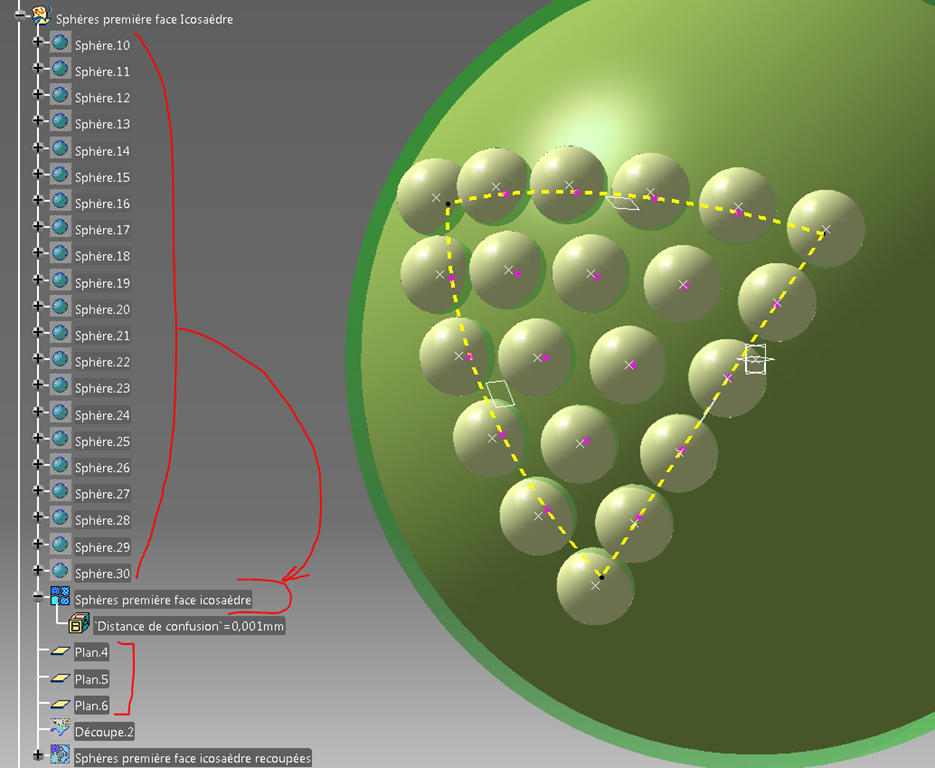
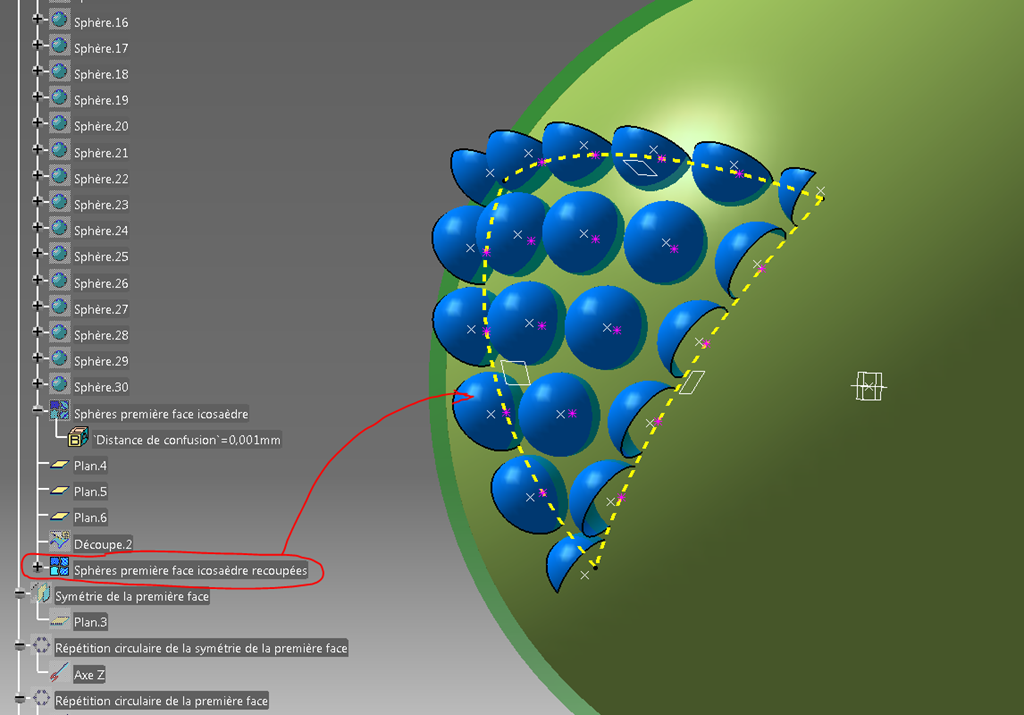
Quatrième étape découpe des sphères

Les sphères qui se trouvent sur les frontières jaunes seront communes avec les faces voisines de l’icosaèdre.
Il convient alors de les couper (l’assemblage de ces sphères) par les plans séparant les faces de l’icosaèdre.

On obtient ces plans facilement. Ils sont définis comme passant par les courbes planes jaunes. Ces plans passent aussi par le centre de la sphère principale.

Voici ce résultat. Il faut maintenant le dupliquer…

Cinquième étape, duplication des sphères.

On va déjà dupliquer ce groupe vers le pôle.
Ici, j’ai fait une image avec la présence de l’icosaèdre de référence.

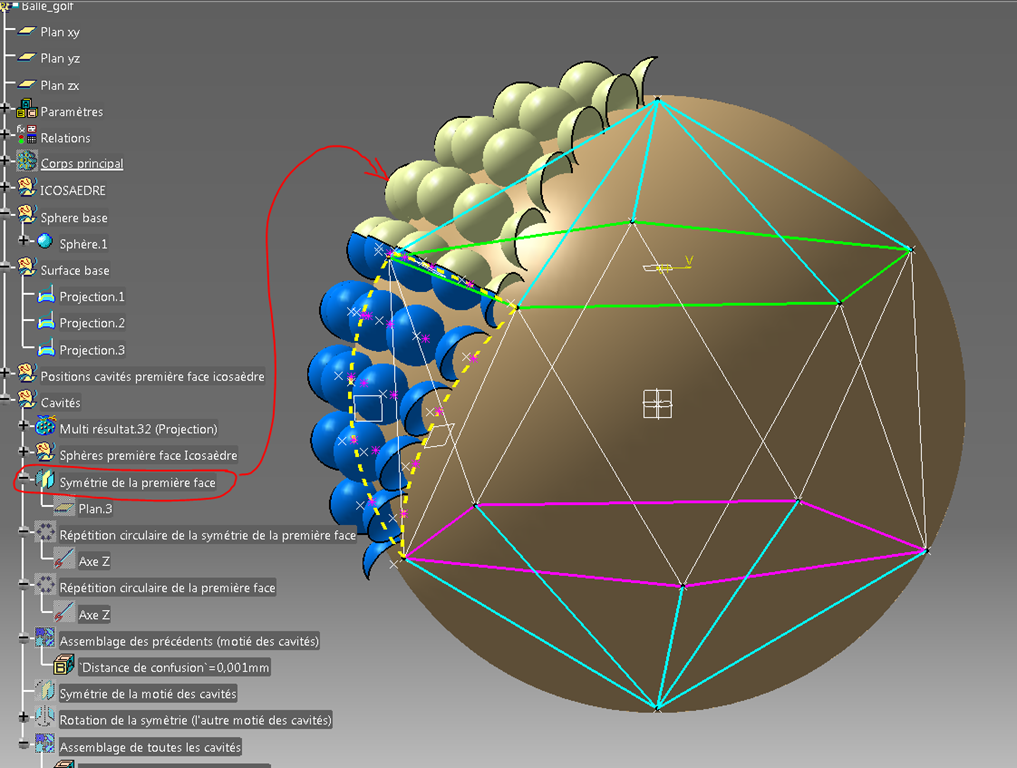
J’en fait ensuite une répétition circulaire (couronne entière, 5 instances soit 72°).

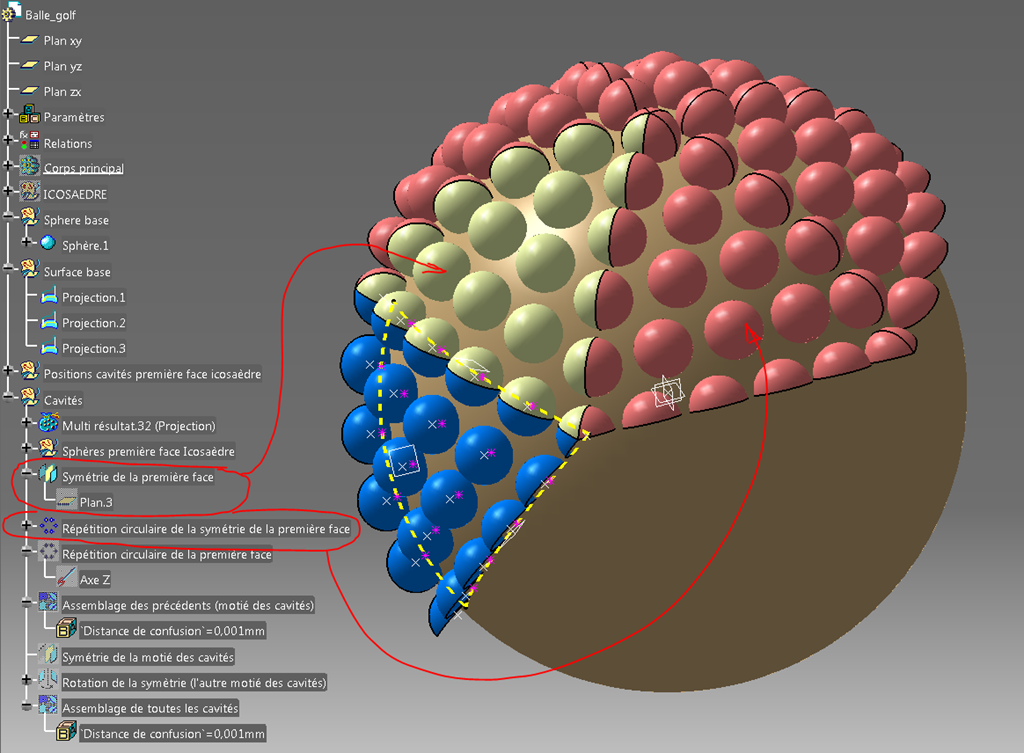
Idem avec le premier assemblage (le bleu).
Puis j’assemble tout ce petit monde et j’en fais la symétrie par le plan équatorial (ici XY).

Ce nouveau groupe symétrisé n’est pas bien calé, il faut maintenant le tourner de 36° sur l’axe Z.

Il y a ensuite assemblage du tout.

Dernière étape, le solide

Tout simple maintenant, il suffit de passer du surfacique au solide par une opération de remplissage pour:

• la sphère de base
• l’ensemble des petites sphères

Une opération booléenne solide de retrait donne le résultat souhaité, une vraie balle de golf !

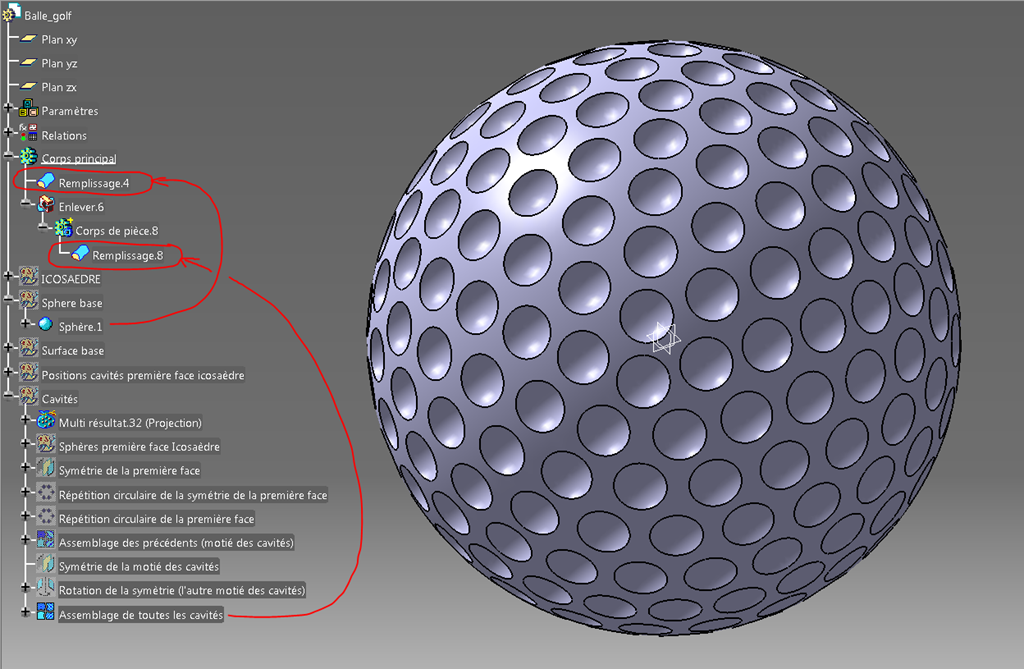
Conclusion

Je pense que cet article est actuellement le seul sur le net montrant la construction en CAO d’une balle de golf dans les règles de l’art.
Certes, ce n’est pas aussi facile qu’une répétition circulaire des cavités mais c’est une construction juste dans le sens où les creux sont uniformément répartis sur la balle comme l’exige les règles de ce sport.

Et vous, comment dessinez-vous les balles des golf ?