Rassurez vous, je ne suis pas du tout matheux et si je me lance aujourd’hui dans la modélisation d’un volume mathématique, ce n’est pas pour la passion des équations mais pour préparer une autre modélisation.
Nous verrons cela dans un prochain article.

Pour le moment, il s’agit de répartir correctement les 12 sommets de ce solide sur une sphère enveloppante.
Le résultat ne sera pas exact au sens mathématique du terme mais suffisamment précis pour être exploitable par la suite.

Il n’y a pas ce genre de chose nativement disponible dans Catia pour créer un tel volume alors…

Comment faire un Icosaèdre sur Catia V5 sans difficulté ?

C’est quoi un icosaèdre ?

Pour faire simple, on peut se représenter ça comme étant deux pyramides (base pentagone) têtes bêches un peu éloignées et tournées de 36° puis raccordées par des triangles.
Tous les triangles de ce solide sont identiques et équilatéraux.

Voir l’article de Wikipédia à ce sujet.

Une des propriétés est que les sommets sont tous sur la sphère circonscrite comme sur cette illustration et je vais partir là dessus pour le modéliser sur Catia.

La modélisation

Je commence par placer une sphère surfacique centrée sur l’origine du modèle (0,0,0) dans un set géométrique.
Son rayon est lié à un paramètre utilisateur (diamètre).

Puis je positionne une esquisse sur un plan parallèle à XY (à une distance inférieure au rayon) et y fait l’intersection avec la peau surfacique.

J’obtiens un cercle grâce auquel je crée les points d’intersection avec des segments radiaux séparé de 72°.

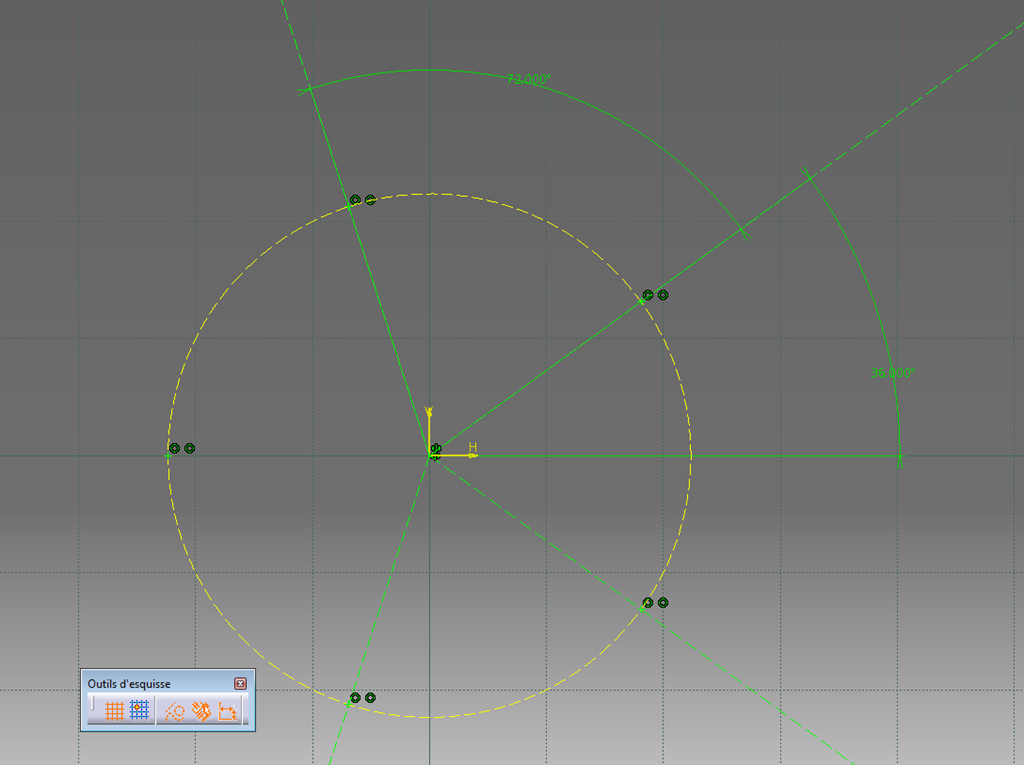
Dans l’esquisse, seuls les points ne sont pas en élément de construction.
On les retrouve donc dans le 3D.
Cela permet de tracer les 5 segments d’un pentagone régulier.

Dans Generative Shape Design, cela se fait avec la fonction « ligne » (option point/point) en désignant les couples de  points de l’esquisse précédente en environnement 3D.

Je crée ensuite l’intersection de l’axe Z avec la sphère (cela donne 2 points) dont un est extrait (celui du haut).

Une symétrie de l’esquisse (les 5 premiers points) puis une rotation permet d’avoir la base de la deuxième pyramide.

Pour faire cette nouvelle entité symétrique, dans le même atelier (GSD), on prend l’outil symétrie (le 3ème en partant de la gauche ci dessous) on sélectionne l’esquisse dans l’arbre puis le plan de symétrie.

Il faut ensuite utiliser l’outil rotation (le 2ème en partant de la gauche) et sélectionner cette symétrie et l’axe de rotation et donner l’angle (36°).

Avec l’outil ligne, je peux ainsi relier les nouveaux points à ceux de l’esquisse du début ce qui génère des triangles (blancs) qui ne sont pas encore équilatéraux.

Voici les deux bases (pentagones vert et rose) et les segments de liaison (blancs).

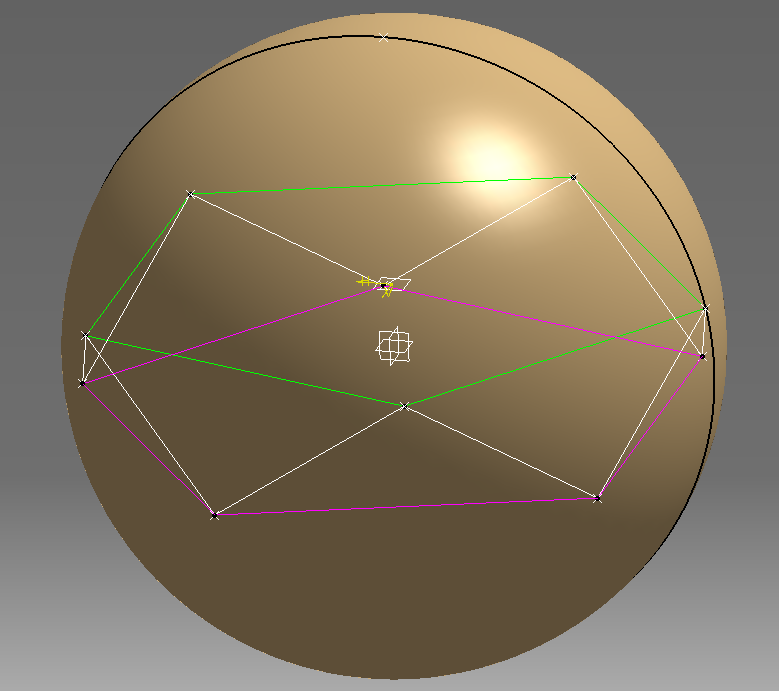
Je peux alors tracer les 5 segments  de la pyramide du haut et ceux du bas après avoir extrait le deuxième point au pôle (bleu).
On a bien le bon nombre d’arêtes mais les triangles ne sont ni semblables ni équilatéraux.
Cela dépend de la position du plan des 5 premiers points.

Placement du plan d’esquisse des points de départ

L’enjeu est ici.
Par un bon positionnement du plan du pentagone vert, on obtient à la fois, l’égalité des longueurs des arêtes et le fait que tous les triangles soient égaux (équilatéraux et de même surface).

Comme je n’ai pas l’équation de la position du plan, j’utilise un algorithme d’optimisation jouant sur la position du plan afin d’obtenir l’égalité de la longueur des arêtes.

Il faut d’abord créer des paramètres utilisateurs pour la longueur de 3 arêtes (une bleue, une verte et une blanche) avec une formule de ce type (ici pour le segment orange).

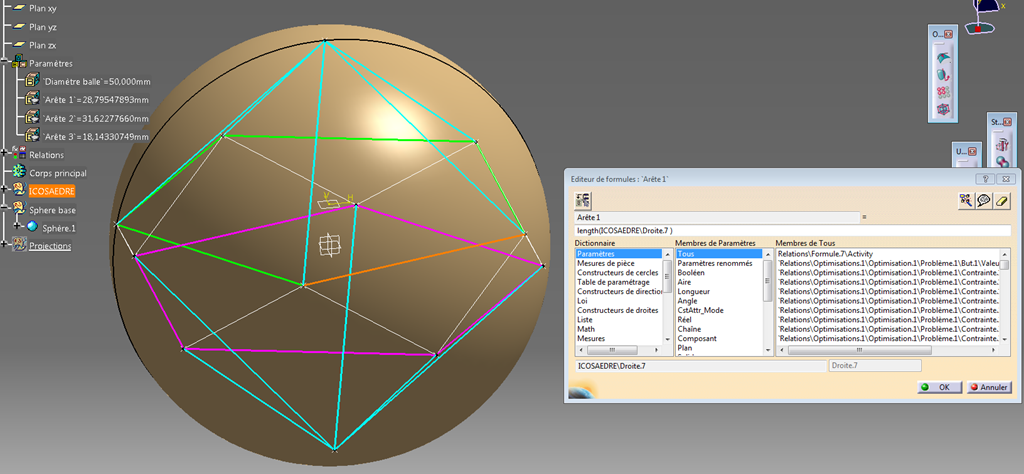
Idem pour les deux autres.
On les retrouve dans le conteneur “Paramètres”.

Les valeurs sont différentes.
Dans l’algorithme d’optimisation, je choisis “Contrainte uniquement”, déclare un paramètre libre (décalage du plan d’esquisse) et …

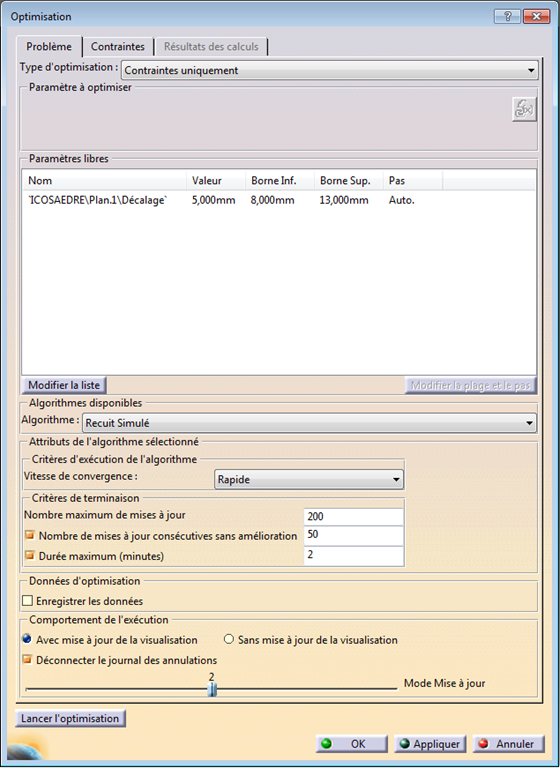
… je crée 3 contraintes comme étant la différence de longueur de deux segments choisis parmi les 3.
Ces écarts doivent tendre vers 0mm.

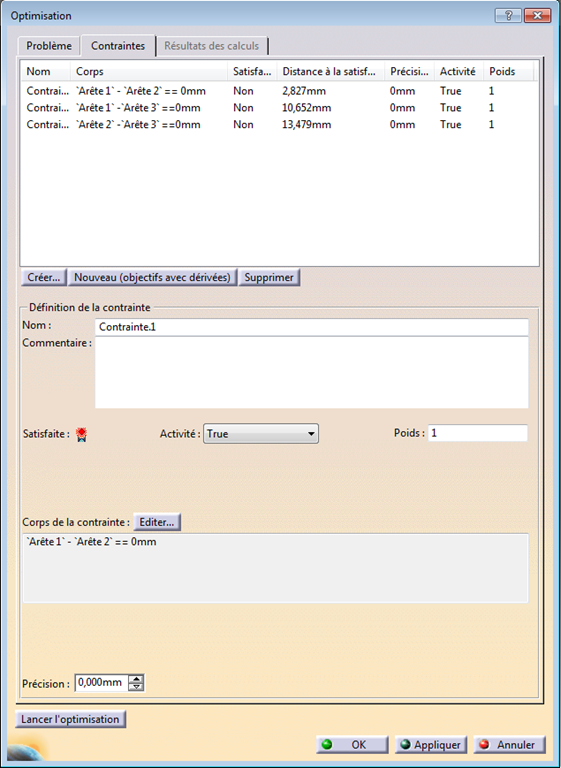
Le résultat donne une égalité des longueurs à très peu de chose près (~1.10-5 mm) identiques.
Toutes les arêtes ont la même longueur et leurs extrémités sont sur la sphère.
On a bien des triangles égaux et équilatéraux.
On peut alors considérer cette construction comme étant un icosaèdre.

Conclusion:

Cet Icosaèdre est une première étape vers la modélisation d’un objet que nous verrons dans un prochain article.
Du fait des symétries, de la relative simplicité de la construction et de l’utilisation de l’optimisation, cette construction n’a pas demandé de grandes connaissances mathématiques.

Et vous, comment construisez-vous un Icosaèdre sur Catia V5 ?