CV5-Utilisez-vous les lois ?

Parmi toutes les bonnes choses présentes dans Catia V5, la possibilité de créer des lois graphiques ou polynomiales sont un atout pour nous concepteurs en tous genres.

Cela nous permet, en plus des paramètres utilisateur, de fournir un nouveau moyen de pilotage de la géométrie.

Dans cet article, nous allons voir les deux types de lois disponibles dans Catia, comment les créer et comment les invoquer.

Deux types de lois dans Catia V5

Il existe deux façons de définir l’évolution d’une variable (en ordonnée) en fonction d’une abscisse.

La première est purement graphique et la deuxième est basée sur une expression mathématique (équation).
Il existe une fonction pour chacune d’elles.

Définition graphique d’une fonction

On aurait pu s’attendre à une interface simple présentant une zone quadrillée dans laquelle on aurait pu manipuler des points de passage, des segments et des arcs de cercle. En fait, il n’en est rien. Catia V5 hérite de V4 ainsi les lois sont définies entre deux entités filaires de l’espace de travail 3D. Pas de grille (quoique ce soit possible) ni d’échelle, on trace comme on veut, oui mais pas n’importe comment.

Même si logiquement un graphique se veut à la base sans unité (jusqu’à ce que l’on donne les unités sur les axes) ici on représente cela en environnement graphique 3D donc tous sera représenté en millimètres et aura pour unité le millimètre.

Étape 1 : Dans un Set géométrique

Je vous conseille de créer un set géométrique rien que pour cela. L’organisation de l’arbre est plus propre, on s’y retrouve plus facilement et cela permet de cacher les éléments de la loi facilement pour dégager l’espace de travail 3D.

Étape 2 : axe des abscisses

Il nous faut une référence, un segment que l’on peut créer soit dans une esquisse ou directement dans le dans l’environnement 3D. Nous le verrons plus tard mais je vous recommande de définir une droite d’une longueur de 100 mm pour l’axe des abscisses.

Étape trois : la fonction

Il nous faut ensuite quelque chose qui puisse définir la fonction. L’idéal est de se placer dans une esquisse et de dessiner par exemple une Spline ou tout autre enchevêtrement de droites et de cercles pouvant définir la fonction du moment que la courbe ne se recoupe pas.
Attention, il faut que le plan de l’esquisse passe par la droite des abscisses. En effet, Catia va mesurer la distance minimale séparant les deux éléments. Si votre plan d’esquisse est à 100 mm en arrière, la distance mesurée sera au minimum 100 mm trop grande.

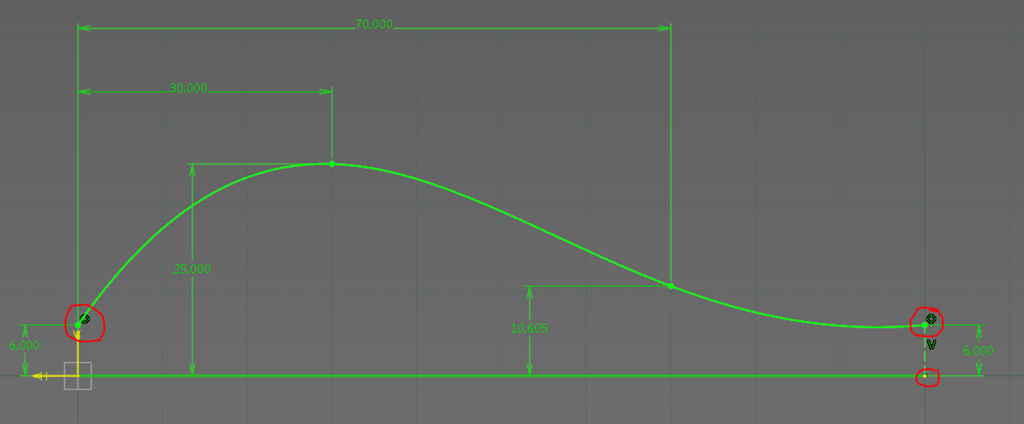
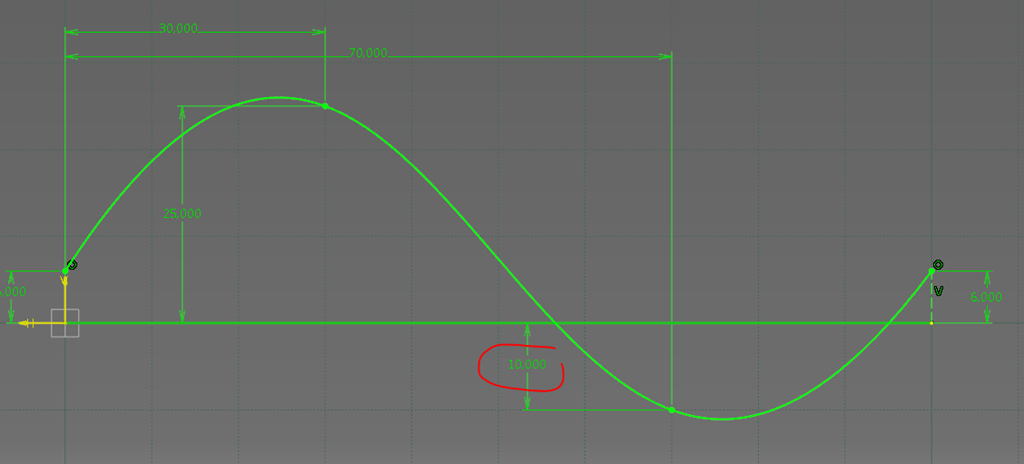
Il est tout à fait possible de croiser l’axe  des abscisses. Catia saura interpréter les valeurs négatives pour les utiliser dans une fonction ou une formule.

Étape 4:  créations de la loi

La fonction Loi se trouve dans l’atelier Generative Shape Design.

L’utilisation est relativement simple, il suffit de donner la référence c’est-à-dire la droite des abscisses et la définition (en fait la courbe définissant la fonction).
Dans la partie analyse de la fenêtre on a un champ “X” d’une valeur égale à 0 que l’on peut incrémenter et réduire grâce aux flèches qui se trouve au bout de la zone. La valeur est en fait un ratio allant de zéro à un en parcourant tout l’axe des abscisses quelle que soit sa longueur.  J’ai pris la précaution de donner une longueur de 100 mm à l’axe des abscisses.  Ainsi lorsque la valeur de  X vaut 1  (100 %) , nous sommes à 100 mm dans le 3D (0.5 = 50%, etc…). C’est plus facile à comprendre que d’avoir un axe des abscisses d’une longueur de 77 mm !

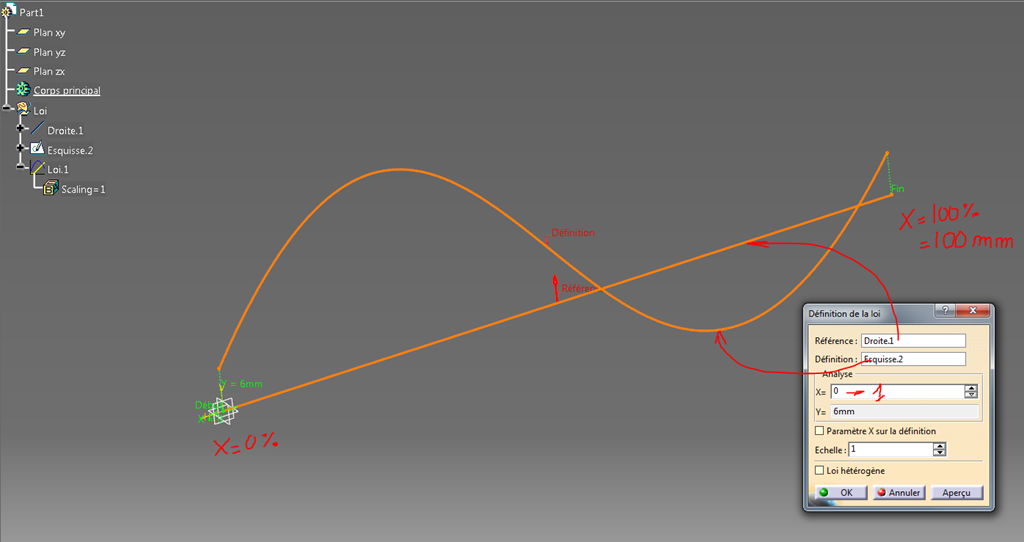
La zone d’analyse de la fenêtre  nous renvoie alors la valeur Y de notre fonction en mm. C’est directement la distance minimale entre un point qui se promène sur l’axe des abscisses et sa projection normale sur la courbe de définition (la fonction).

Et l’échelle alors ?

En effet, il y a un champ pour rentrer une échelle.
Comme dans n’importe quel graphique, cela permet de faire rentrer la courbe dans la feuille de papier.
Oui, c’est vrai mais ici l’espace de travail, puisque nous avons dessiné notre abaque dans le 3D, est gigantesque et il n’y a pas de problème de place.
Pourquoi alors ?
Imaginez que vous ayez besoin d’une courbe qui représente la puissance d’un moteur d’automobile exprimé en Watt. Vous aurez alors des valeurs de l’ordre de 90 000 Watt que vous devrez retranscrire directement en mm donc 90 000 mm (90 m) à coté d’un modèle d’une pièce de moteur faisant quelques centaines de mm. Il faudra alors zoomer et dézoomer beaucoup pour accéder de temps à autre à votre courbe.
On joue alors sur le facteur d’échelle. 90 mm avec une échelle de 1000 feront 90000 mm mais ce sera contenu dans un espace proche (plus besoin de dézoomer pour retravailler la courbe).

Étape 5 : Changer d’unité

C’est bien pratique tout ça, je demande à Catia de me retourner la valeur de mon abaque à 44% (0.44) et je récupère 14.1767 mm.

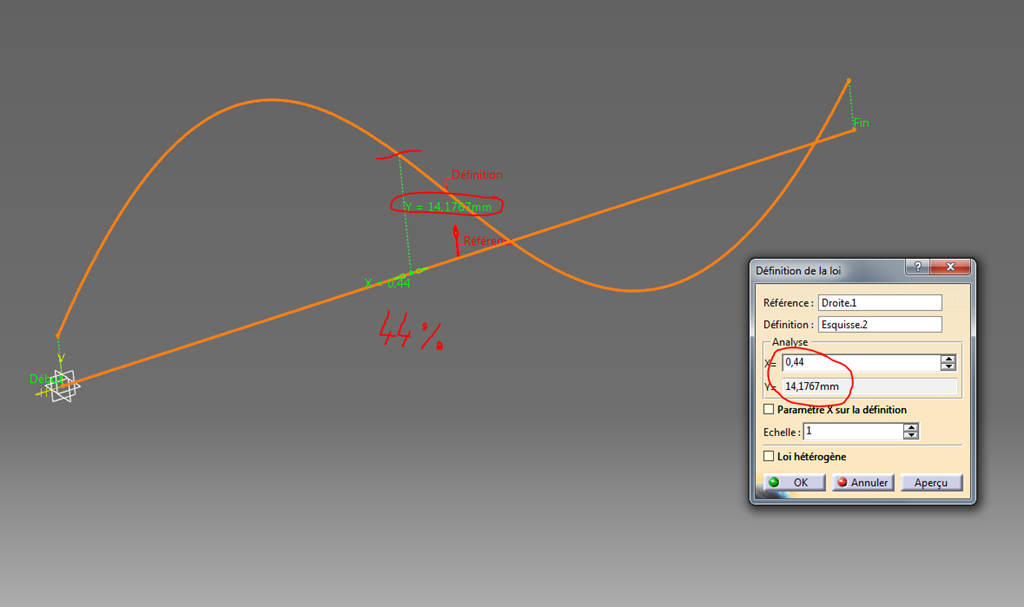
Et bien oui, puisque nous avons dessiné notre courbe dans l’environnement 3D nous étions contraints de manipuler des longueurs (des mm) mais comment faire pour décrire une courbe qui retournerait des degrés ou encore des Watt ?

C’est prévu !
C’est ce que l’on appel ici une loi hétérogène.

Cliquons sur le bouton “loi hétérogène” la fenêtre s’agrandit et deux boutons apparaissent.
Le premier, “unité appliquée” appliquée indique “Aucune (Ratio)” et le deuxième “Unité de mesure”
indique “millimètre”.
Ce premier bouton vous permet de fixer l’unité pour la sortie. Ici sans unité vous aurez remarqué que dans la fenêtre et sur la vue graphique, il n’y a plus d’unité derrière Y (auparavant  c’était des mm). On peut aussi choisir parmi quelques possibilités dont une sortie en angle (degré). C’est toujours pratique.

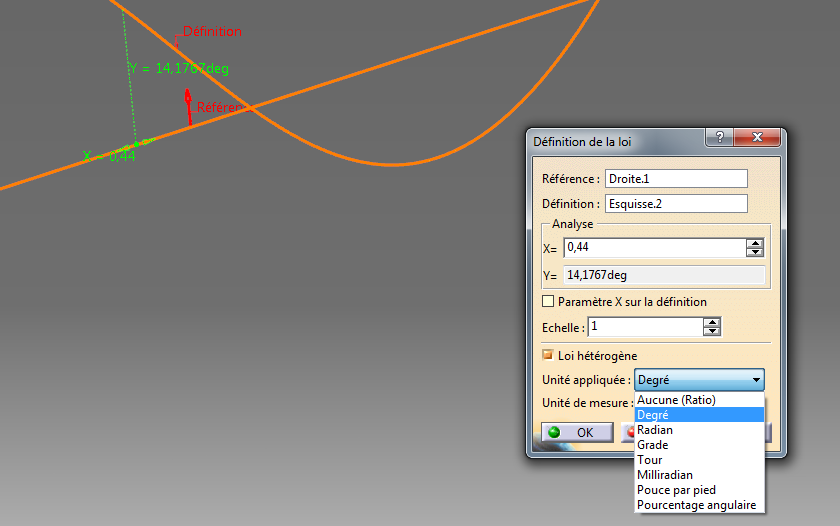
Vous voyez alors que la valeur Y est exprimée en degré et plus en mm.

Le deuxième bouton est moins intéressant. Il permet de “tricher” sur l’unité de mesure lorsque Catia évalue la distance entre des deux éléments.
Supprimons “ l’unité appliquée ” nous retrouvons un Y de 14.1767  (sans unité) homogène à nos 14.1767 mm physiquement présent dans le 3D. Changeons maintenant d’unité de mesure en passant des mm au m.
On a alors une valeur en retour de Y mille fois plus petite (0.0141767). C’est la mesure de nos 14 mm exprimée en m.

Récupération d’une valeur issue d’une loi

OK pour les angles mais si je veux des Watt en sortie ?

Dans ce cas, il vaut mieux faire une sortie sans unité et multiplier par l’unité souhaitée dans une formule par la suite comme ceci:

On peut par exemple faire une nouvelle loi pour décrire l’évolution de la puissance avec en ordonnée des mm équivalents à des kW:

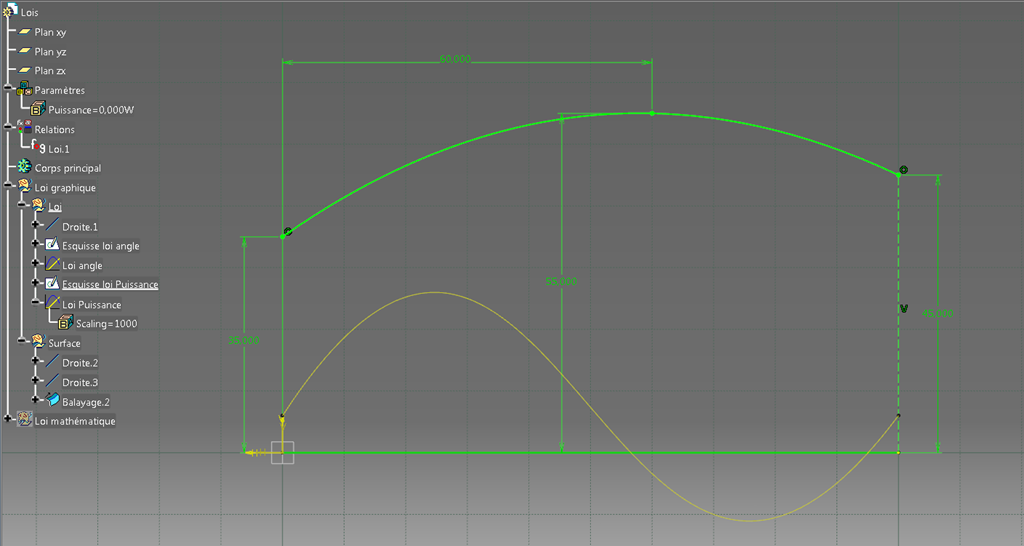
Puis créer une nouvelle loi sans unité avec une échelle de 1000 en sortie.

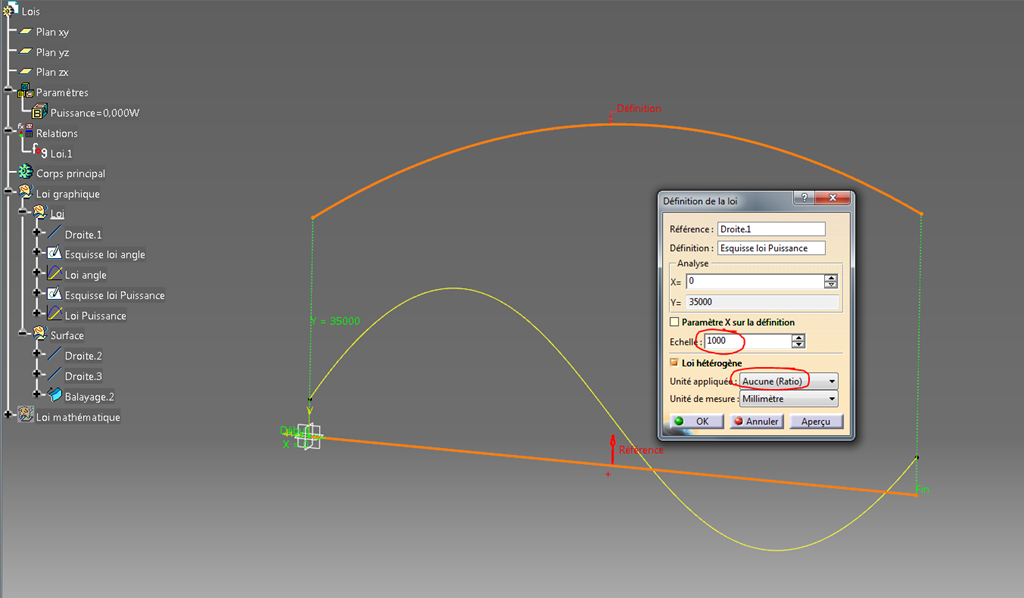
On a alors deux lois basées sur la même référence et définies par deux courbes différentes.

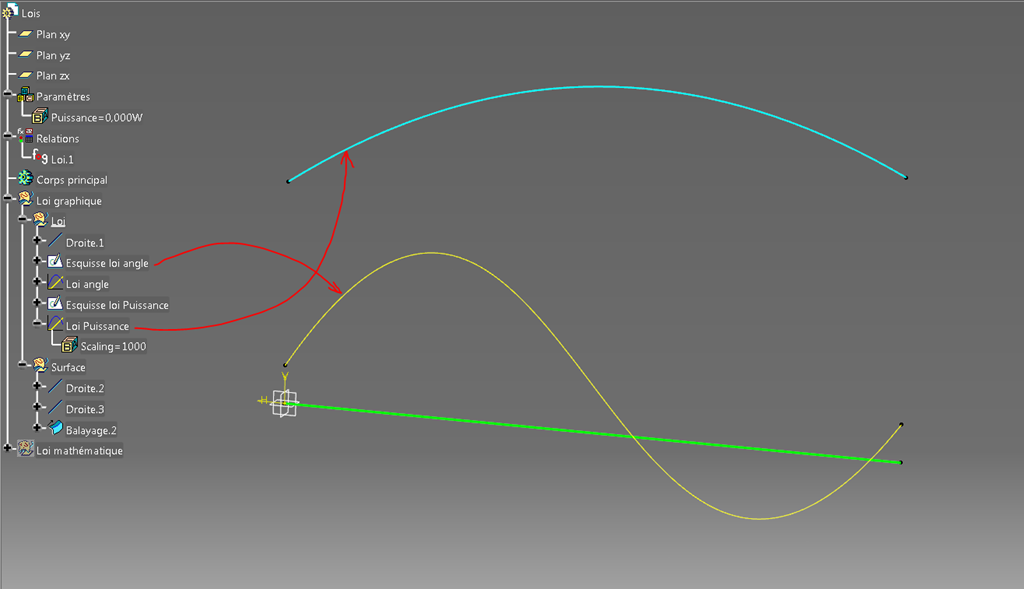
Ajoutons un paramètre de type puissance (Puissance “électrique” dans la liste, oui c’est bizarre).

Puis un autre paramètre de type “Proportion” pour piloter l’entrée c’est à dire la valeur sur l’axe des abscisses.

Puis ajoutons une formule au paramètre puissance comme ceci:

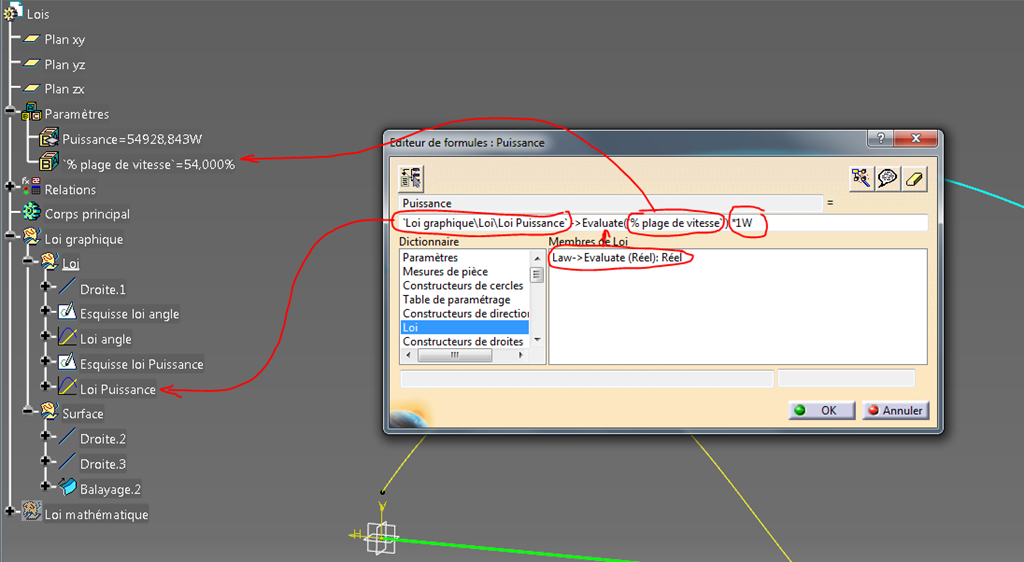
Cela permet d’évaluer la loi en demandant la sortie (valeur en ordonnée) pour une seule valeur entrée en abscisse (ici 0.54). Ne pas oublier de multiplier par 1W car il n’y a pas d’unité à la sortie de la loi et il nous faut des Watt pour alimenter le paramètre de puissance.

 

Une application pour voir:

Il existe dans Catia des fonctions dans lesquelles il est possible d’invoquer une ou plusieurs lois de façon à piloter un rayon, un angle, etc…
On les repères grâce à la présence de ce bouton.

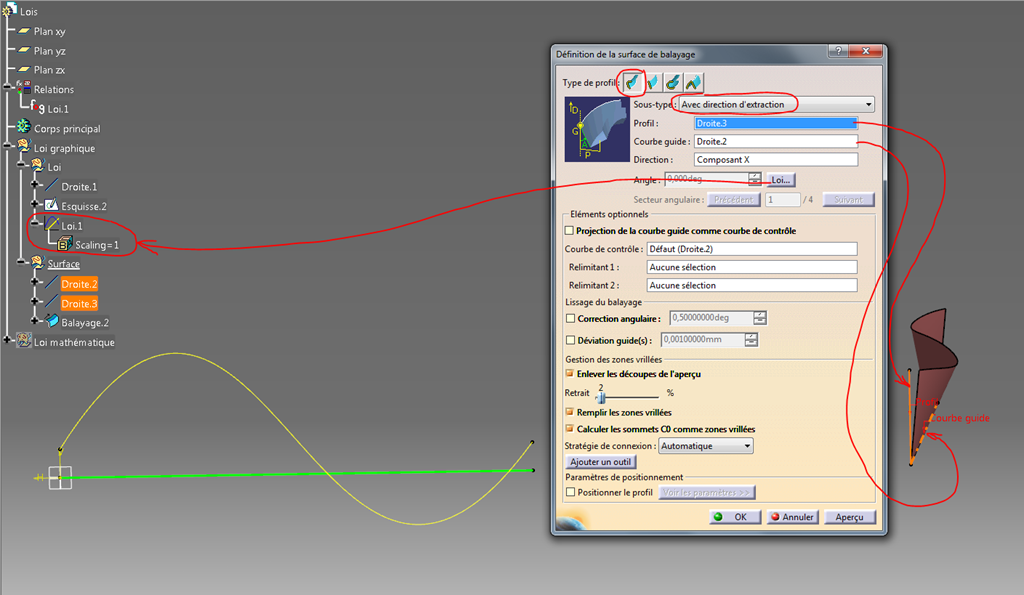
Dans l’exemple suivant nous allons réaliser le balayage d’un profil suivant une droite en faisant varier l’angle.
Dans un premier temps, nous utilisons la loi telle-quelle avec une sortie en angle (deg) et un facteur d’échelle de 1.
Le profil balayé est un petit segment (rose) le long d’un guide (segment blanc).
L’angle est contrôlé par la loi lorsque l’on désigne la loi dans l’arbre après avoir appuyé sur le bouton loi.
On voit que le ruban commence par un angle positif (ce sont les 6 degrés du début de la loi). Le ruban est bombé du côté droit (angle positif) puis passe de l’autre coté comme l’impose la courbe de la loi.

Changeons l’échelle dans la loi (passons de 1 à 5) pour amplifier la chose.
La loi n’est pas transformée mais la sortie est multipliée par 5 ce qui se répercute sur le ruban.

Conclusion –> attention

Prenez toujours un grand soin à vérifier ce que donne la sortie en manipulant X dans la fenêtre pour voir si la sortie est d’une part dans la bonne unité (mm, deg ou sans unité) et si le niveau de sortie est celui que vous attendiez.

Définition mathématique d’une fonction

Il ne s’agit pas de la même commande.
Si la première se trouvait dans l’atelier Generative Shape Design, on trouvera celle-ci dans tous les ateliers puisqu’elle dépend directement de Knowledge.

Éditeur de lois mathématiques

Il est souvent caché par le bouton “Table de paramétrage”. Si l’on clique dessus, une première fenêtre s’ouvre puis une deuxième après avoir validé par Ok.

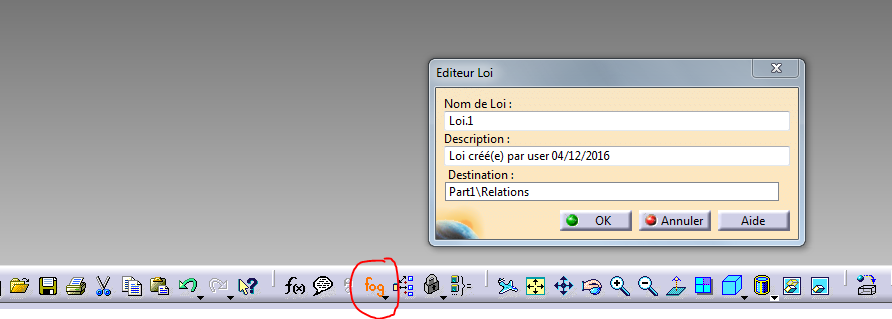
Nous voilà alors dans l’éditeur de loi mathématique.
Il ressemble beaucoup à l’éditeur de formule classique de knowledge mais possède en plus une zone dans laquelle nous allons pouvoir définir des variables d’entrée et de sortie permettant de balayer l’équation définissant notre loi.

Nous commençons donc par là en créant dans cette zone un paramètre de type Angle et un autre de type Longueur.
Je les renomme A pour l’angle et X pour la longueur.
Nous allons pour illustrer créer une loi sinusoïdale puis la tracer.

A la base la fonction mathématique est du type X=Cos(Angle) mais nous allons la retoucher pour obtenir quelque chose de positif avec 12 périodes.

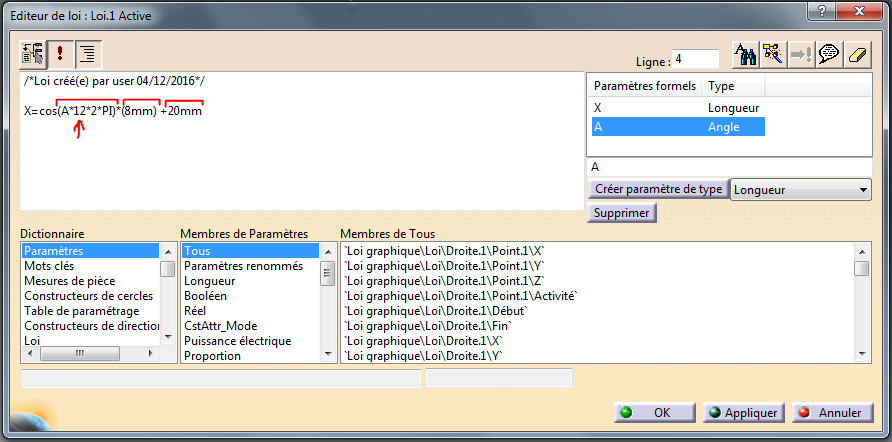
Dans le premier crochet (il s’agit du contenu de la fonction cosinus) nous allons multiplier l’angle par 2Pi pour avoir quelque chose de trigonométriquement convenable (une période sur l’étendue de l’abscisse) et également par 12 pour avoir 12 périodes sur l’étendue de l’abscisse au lieu de 1.
Dans le deuxième crochet nous multiplions ce premier résultat par 8mm. Cela augmente l’amplitude de la sinusoïde (*8) et donne une unité de longueur (mm) à la valeur qui jusque là n’avait pas.
Dans le troisième crochet, nous décalons la sinusoïde de 20mm de façon à ce que toutes les valeurs soient positives.

A ce stade, rien de graphique ne nous permet de vérifier si notre équation est bonne.
Il faut alors la tracer grâce à une fonction qui autorise l’utilisation d’une loi.

Le plus classique est d’utiliser courbe parallèle de Generative Shape Design.

et de prendre comme référence une droite de 100 mm de longueur (ça tombe bien on en a déjà une. Ici je l’ai copiée collée dans le set géométrique “Loi mathématique”).

Derrière le bouton loi, il y a cette fenêtre montrant ce que nous aurions aimé voir juste avant dans knowledge.
Dans cette fenêtre, il est d’ailleurs possible de définir succinctement d’autres lois mais ici il s’agit d’une loi de type Avancée car définie au préalable par une des deux méthodes de création d’une loi.

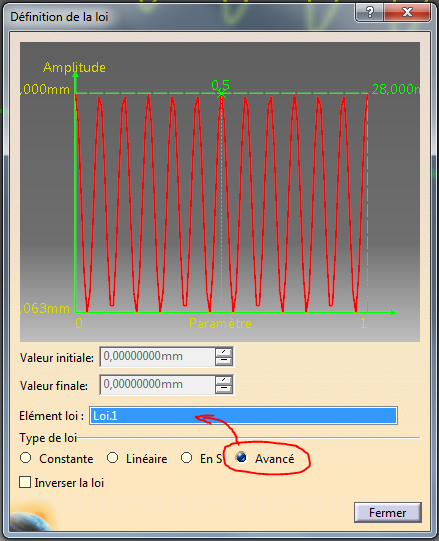
En tout cas, nous avons une idée de la visualisation graphique de notre fonction et nous pouvons l’appliquer à une entité plus complexe.

Application sur un balayage.

Il nous faut une courbe guide. J’ai ici fait une Spline dans l’espace à l’aide de points placés au pif (et oui ça m’arrive !).

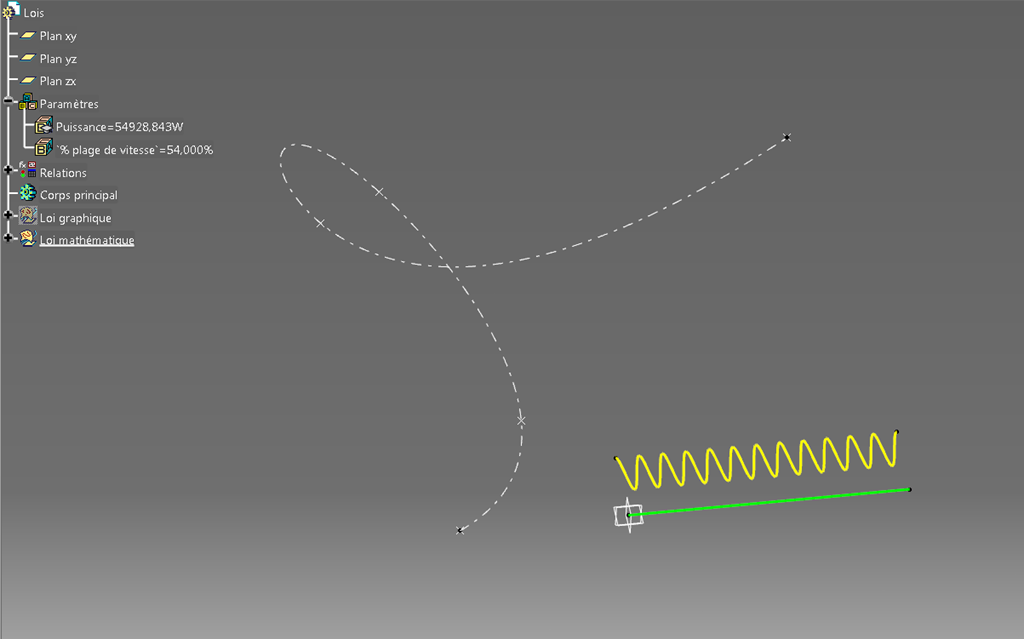
On peut alors lancer la fonction balayage d’un profil circulaire (c’est le plus rigolo) et pointer la courbe guide et cette loi en guise de rayon.

Voilà un résultat qui n’est pas sans rappeler la forme d’un intestin. En tout cas, plus mécaniquement, c’est toujours pratique pour dessiner une gaine anti-poussière en caoutchouc annelé sur un câble.
Vous remarquerez qu’il y a bien autant de bosses entières qu’il n’y en a sur la sinusoïde.
Catia s’est débrouillé pour mapper tout cela le long de la Spline en dessinant un grand nombre de cercles normaux à ce guide avec un rayon correspondant à la valeur de la loi le long de l’abscisse (en proportion car rappelez vous bien qu’il s’agit d’un pourcentage de l’axe des abscisses).

Conclusion sur cette méthode mathématique.

Définir une loi de cette façon peut être pratique lorsque l’on doit exprimer une forme de façon juste à l’aide d’une formule mathématique.
On peut par exemple dessiner un projecteur dont la forme doit obligatoirement être parabolique.

Conclusion générale sur les lois

Voici deux outils indispensables si vous devez modéliser une géométrie répondant soit à des abaques (première solution = graphique) soit à des formules mathématiques (deuxième solution = mathématique).
Si certaines fonctions admettent l’utilisation d’une loi, il n’en va pas de même pour la plupart des outils de Catia V5.
Vous pourrez tout de même, grâce à une formule, obtenir d’une loi une valeur en retour d’une position sur l’axe des abscisses (de 0 à 1).

Voilà pour cet article, n’hésitez pas à partager votre expérience de Catia dans les commentaires ou partager cela sur les réseaux sociaux.