Certaines personnes comme moi sont fascinées par les solutions techniques que la nature à mise en place au cours de l’évolution.
La forme de l’œuf illustre peut être parfaitement cette fascination tant elle a su étonner nombre de générations par son extraordinaire faculté de résister à la compression axiale.
Dans cet article, je me propose de réaliser un petit montage numérique pour estimer l’écart de tenue entre un œuf et une sphère en compression.

Sommaire
Écart de tenue en compression d’un œuf et d’une sphère sur Catia V5
Je n’ai pas lu grand chose sur le net à ce propos hormis quelques écrits de passionnés trouvés sur ce site. Merci à eux.
Je n’ai pas pour prétention de fournir ici une étude qualitative et quantitative au sujet de la tenue de la coquille de l’œuf.
Cet article est là pour montrer comment organiser l’ensemble des modèles afin de réaliser ce calcul sur Catia V5. Autant le faire alors sur un sujet ludique et puisque qu’il s’agit uniquement de mettre en évidence un écart et non de trouver une valeur de contrainte juste, j’ai abandonné tout espoir de trouver les propriétés physiques du matériau de la coquille (calcaire) et opté pour un acier !
L’œuf calculé est donc un œuf en acier d’une épaisseur de 0.4 mm.
La sphère est faite de la même matière avec la même épaisseur.
Vidéo de l’article
Préparation du modèle
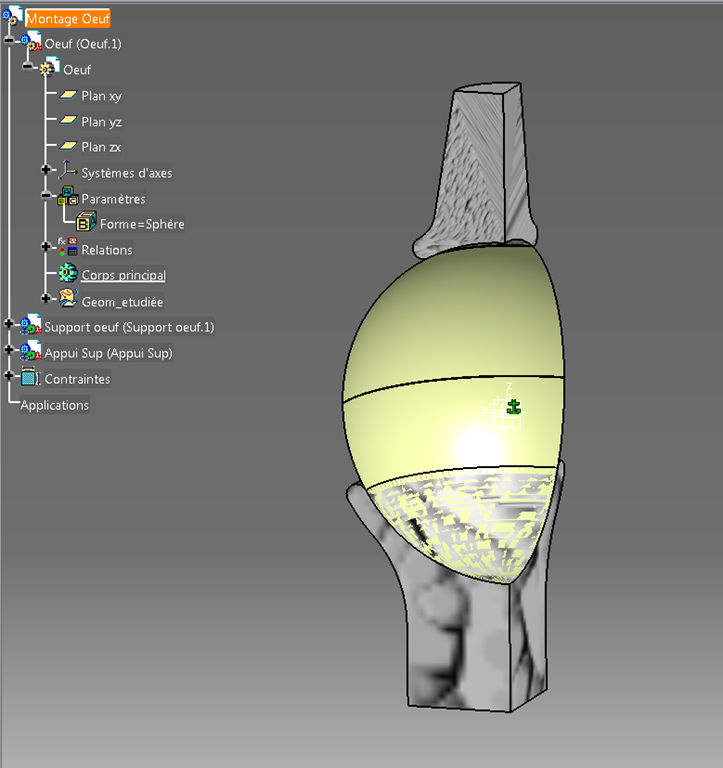
La partie étudiée (Catpart Oeuf).
Celle-ci sera une coque (maillée avec des éléments coque, pas un œuf à la coque : ) ).
Il convient donc de modéliser cela en surfacique et il est inutile de faire un solide.
Ce modèle est une Catpart et est au centre de l’étude (les autres modèles en dépendront).
J’ai introduit une astuce permettant de passer de la géométrie “Œuf” à la géométrie “sphère” en un clic sur un paramètre utilisateur de type chaîne à choix multiple.
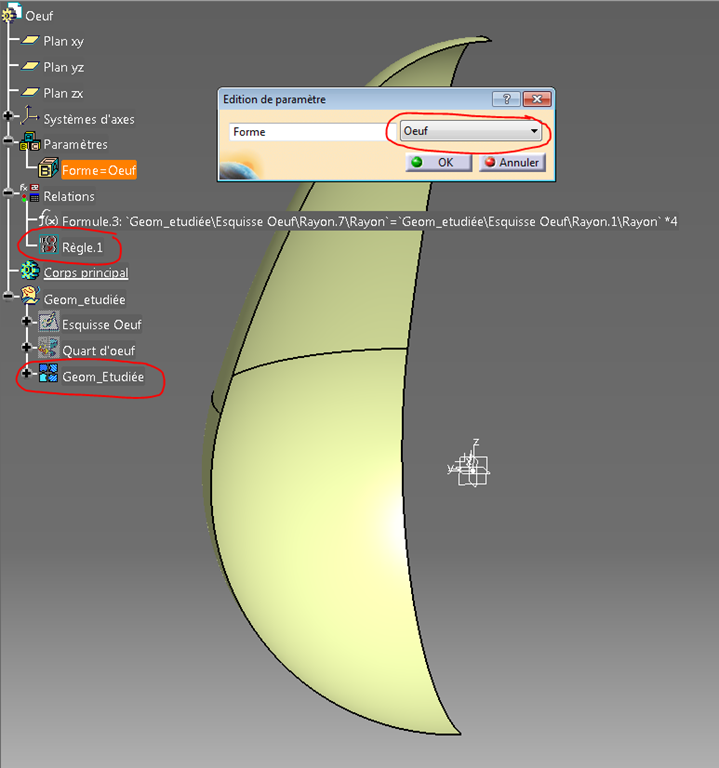
Derrière se trouve une règle permettant de modifier les valeurs des cotes se trouvant dans l’esquisse générant la surface (révolution d’un quart d’œuf).
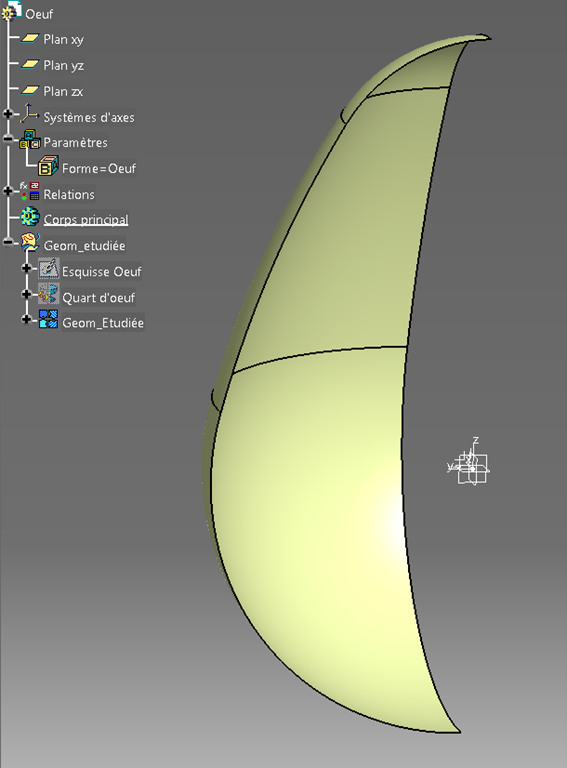
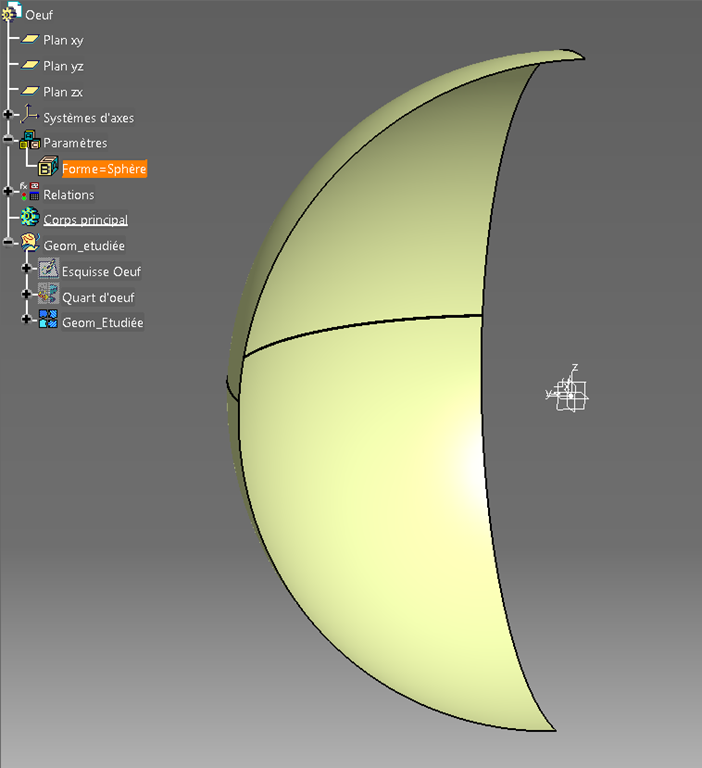
L’esquisse est assez simple.
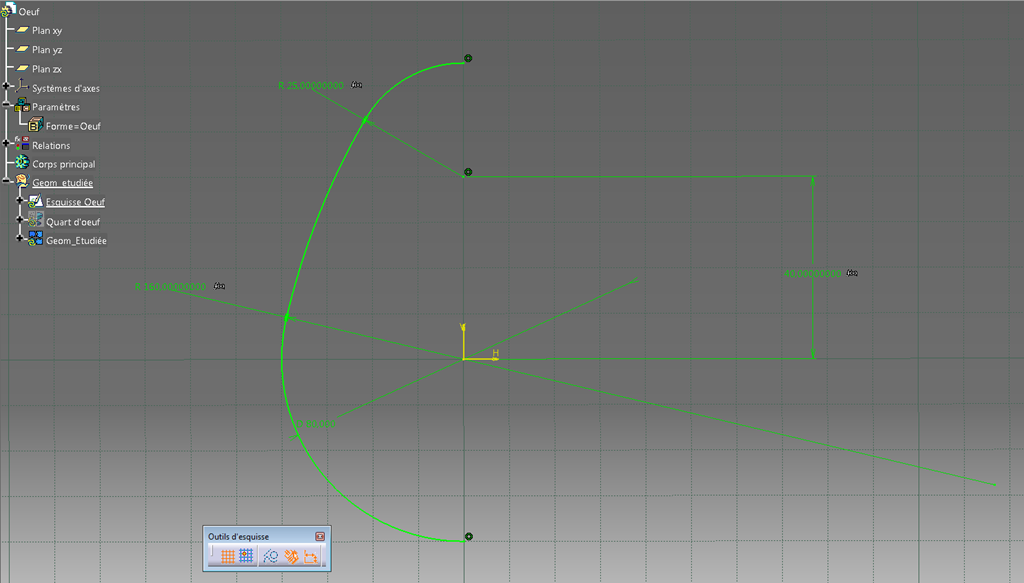
et est donc pilotée par cette règle:
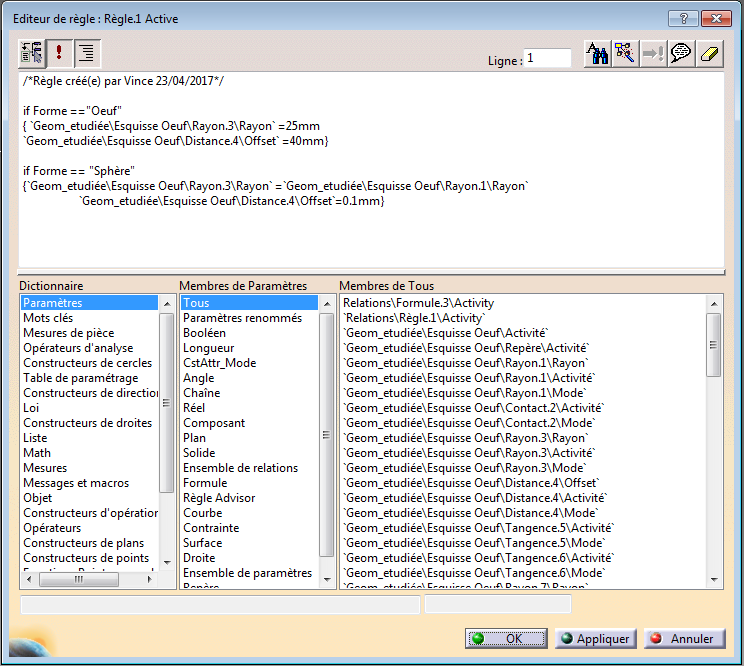
L’assemblage (Catproduct)
La catpart de l’oeuf est ensuite mise dans une Catproduct et immobilisée dans l’espace (fixité).
Puis deux Catpart vides sont ajoutées et liées à la première (l’œuf) à la fois en position (fixité relative) et parce que la forme de l’œuf (l’esquisse) est projetée dans ces nouvelles Catpart pour construire leurs propres esquisses.
On a alors des liens entre les catpart via la catproduct.
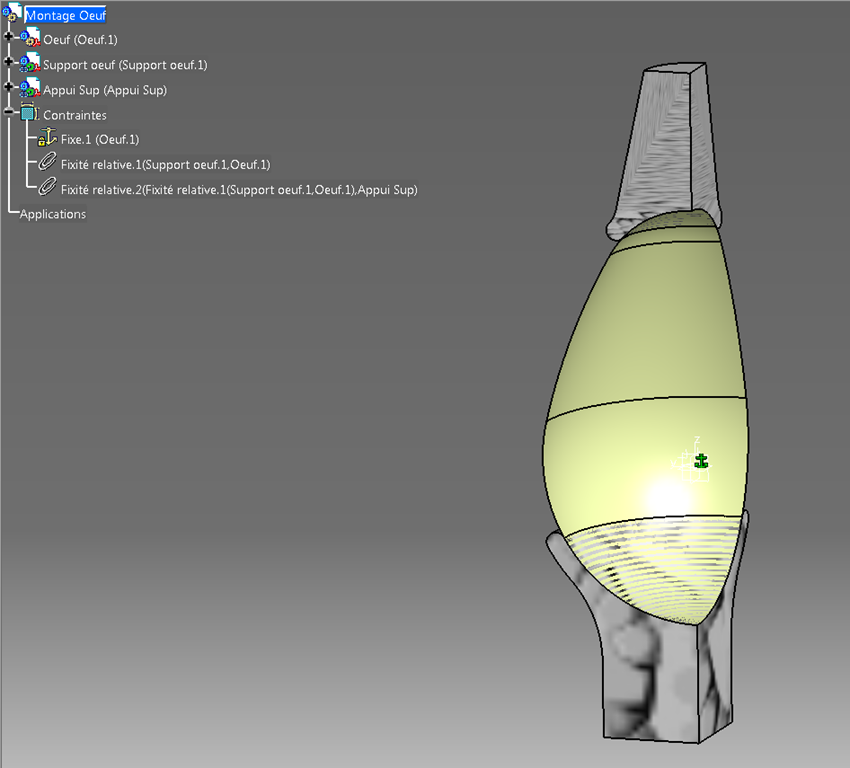
On a alors des liens multi-modèles entre les catpart via la catproduct.
Support Œuf (en bas)
Cette pièce est un solide. L’esquisse s’appuie sur la courbe projetée depuis la catproduct.
Elle sera affublée d’un matériau très souple (module d’young = 5000 MPa) pour ne pas appuyer de façon singulière sur l’œuf.
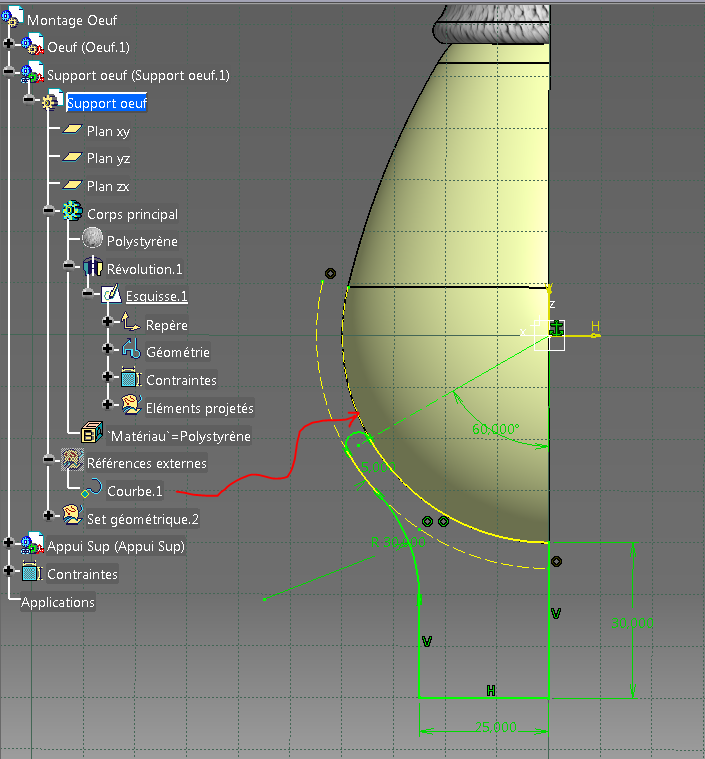
Appui sup (en haut)
Cette pièce est aussi un solide. L’esquisse s’appuie sur la courbe projetée depuis la catproduct.
Elle sera affublée d’un matériau très souple (module d’young = 5000 MPa) pour ne pas appuyer de façon singulière sur l’œuf.

Cycle de mise à jour
La seule variable géométrique est donc le choix entre l’œuf ou la sphère.
Lors du changement (obligatoirement dans la Catpart Oeuf) les autres pièces (catpart) ne détectent pas ce changement car elles ne sont pas directement liées à la catpart “Œuf”.
Il faut mettre au préalable la product à jour. Ceci entraîne alors une mise à jour des Catpart “Support” et “appui sup”.
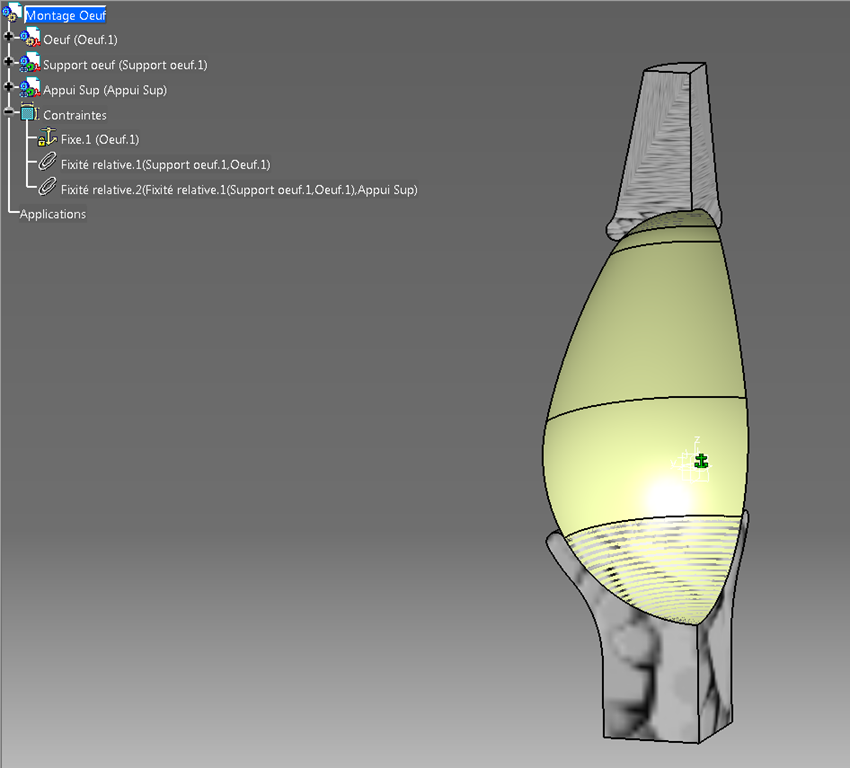
Le modèle de Calcul
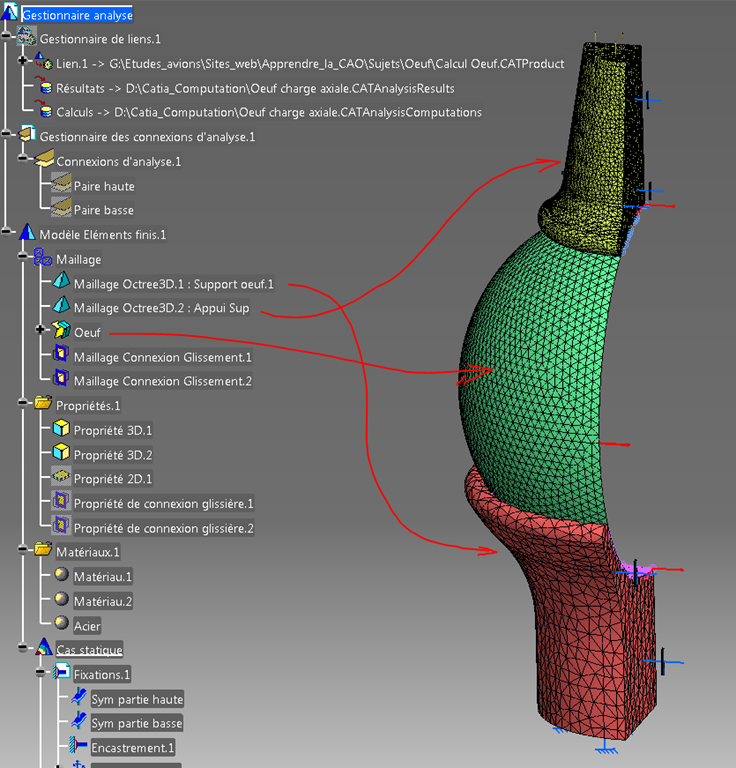
Maillages
La Catanalysis est en lien avec la Catproduct.
Les deux maillages solides Octree se construisent automatiquement car les solides sont les corps principaux des catpart.
Pour l’oeuf, il n’y a pas de solide mais une surface que j’ai maillé en coque (éléments Quads) avec l’atelier Advance meshing tool. (rien de particulier ici).
Matériaux et propriétés physiques
Les deux solides héritent du matériau souple que j’avais appliqué dans Part Design.
La propriété physique solide est déjà renseignée.
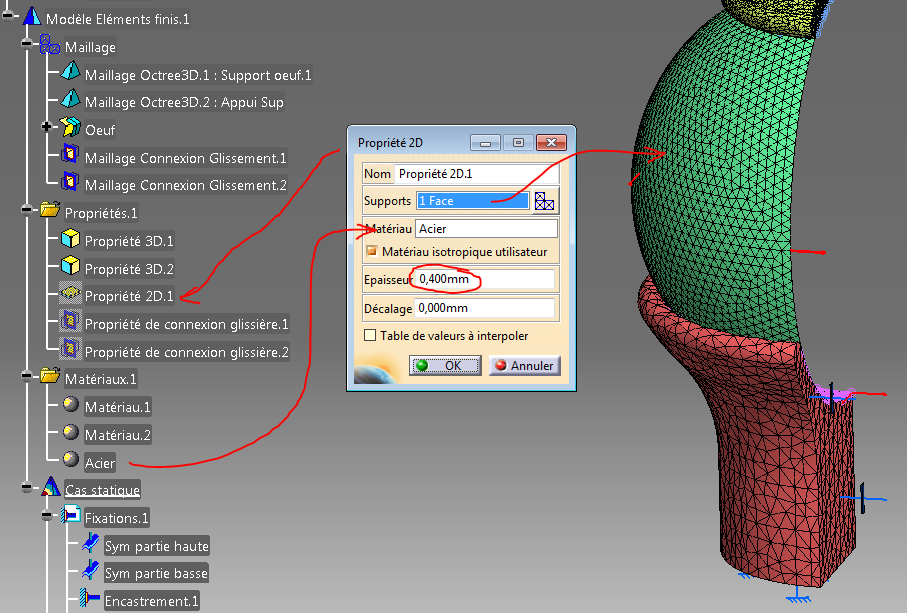
Il faut par contre créer un matériau utilisateur pour la coque.
J’utilise tout simplement le matériau Acier du catalogue.
Puis ajouter une propriété physique de type coque et associer le maillage et le matériau utilisateur.
Épaisseur 0.4 mm comme un œuf de poule.
Les paires de contact
J’ai opté pour un calcul avec des contacts.
Il faut donc commencer par désigner des paires comme ceci en désignant les faces en vis à vis.
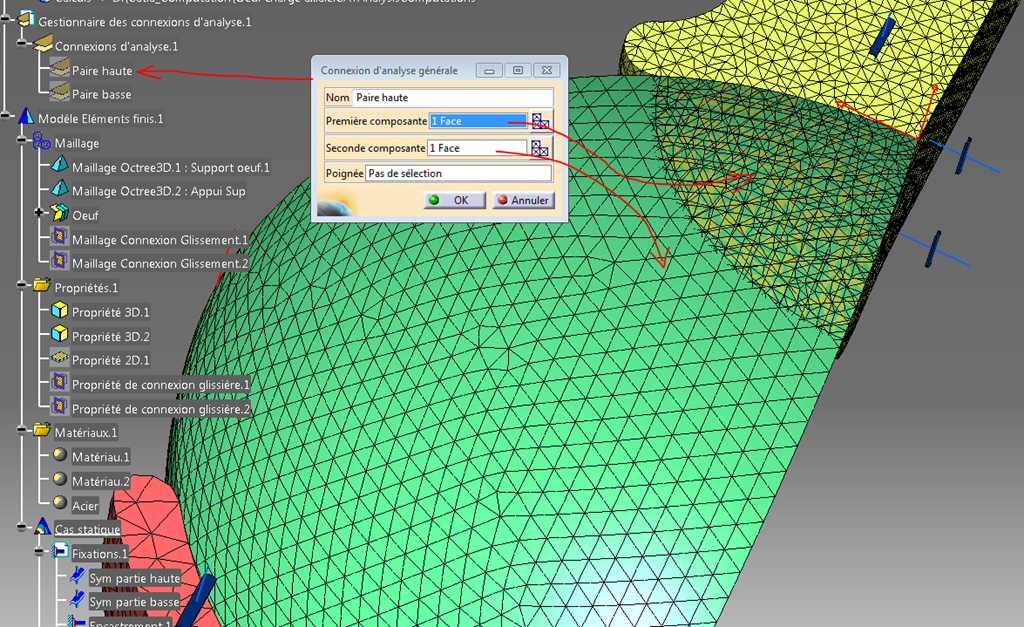
La même chose pour la partie basse.
Puis de préciser qu’il s’agit d’un contact glissant:

Les fixations
Dans un repère global, j’ai placé des conditions limites de glissement sur les faces des plans de symétrie des solides et un encastrement en bas.
Pour l’œuf surfacique, j’ai sélectionné les arêtes et les ai bloquées en thêta dans un repère cylindrique utilisateur.
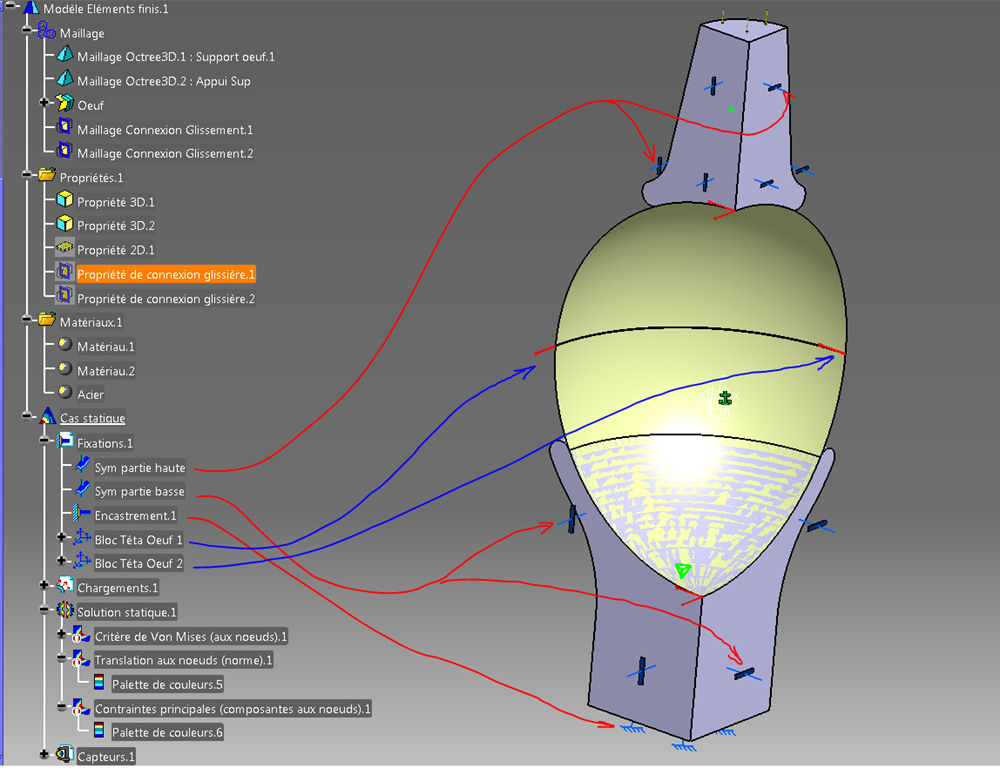
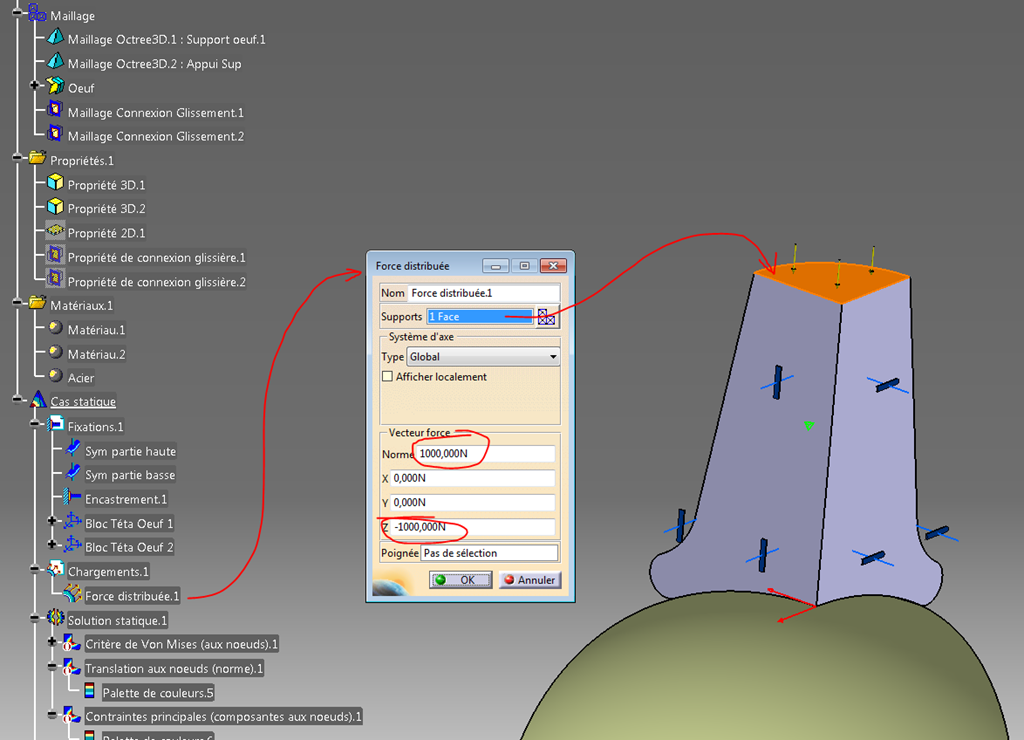
Le chargement
La charge est fixée ici arbitrairement à 1000 N sur la face supérieure de l’appui dans la direction Z vers le bas.
Résultat du calcul (en relatif)
Tout d’abord, je ne regarde ici que la contrainte maximum principale au point d’intégration en peau sup et inf de la coque.
Pour les deux géométries la contrainte est orientée de la même façon (traction circonférentielle) comme ceci:

Un écrasement aux pôles induit donc une traction circonférentielle dont la valeur varie selon l’éloignement des pôles.
Dans les deux modèles, on observe que valeur de la contrainte présente un minimum à proximité de l’équateur.
J’ai jugé bon de comparer ces deux modèles sur cette valeur car rechercher la contrainte la plus élevée sur chaque modèle revient à post-traiter aux conditions limites.
Quoi qu’il en soit l’ordre de grandeur du coefficient entre les deux modèles (x4) donné plus bas se tient si l’on sonde les deux pièces dans des zones similaires de la partie géométriquement différente.
Ci dessous voici les mêmes post-traitements pour la sphère et pour l’oeuf. L’échelle de valeurs est fixe et identique pour les deux modèles.
(Voir la vidéo)
Pour la Sphère:
La valeur minimale de la contrainte maximum principale (post-traitement de la coque Sup et Inf) est d’environs 40 MPa.
La zone rouge n’est pas prise en compte car elle est proche des conditions limites (contact d’appui).
On voit que la contrainte circonférentielle diminue depuis cette zone rouge (80 MPa au bord de cette zone) vers “l’équateur”, passe par un minimum (40 Mpa) puis ré-augmente symétriquement vers l’appui inférieur.
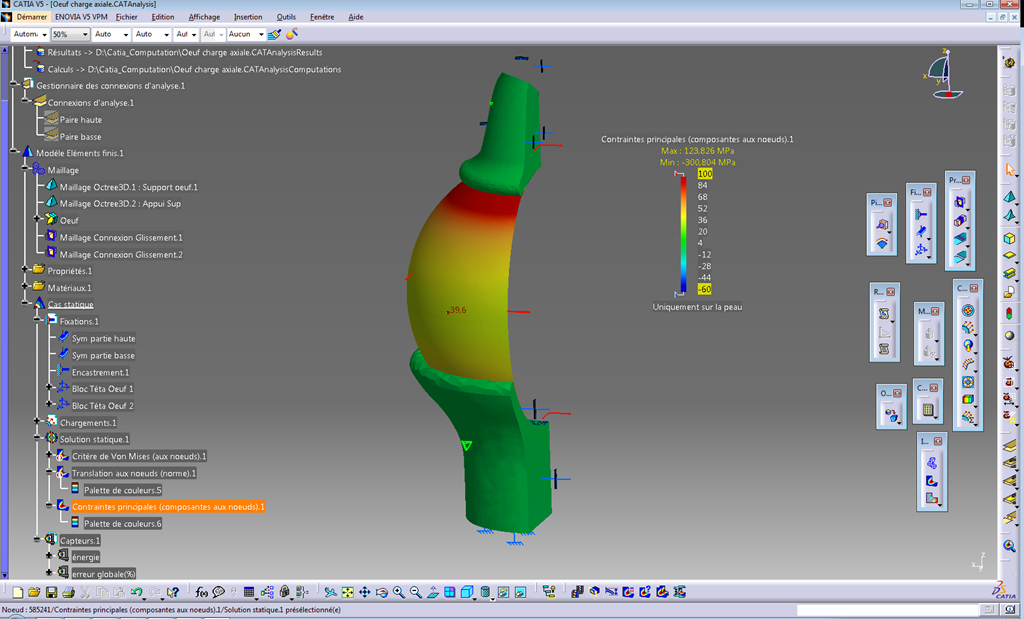
Pour l’oeuf :
La valeur minimale de la contrainte maximum principale (post traitement de la coque Sup et Inf) est d’environs 10 MPa !
Contrairement à la sphère, la partie située entre “l’équateur” et l’appui supérieur présente une zone sensiblement conique dont la contrainte est quasi constante et de l’ordre de 15-20 MPa.
Elle présente un minimum de 10 MPa avant d’atteindre “l’équateur”.
Dans la partie basse (sous “l’équateur”) on retrouve les mêmes valeurs de contrainte que sur la sphère. Ceci est logique puisque la géométrie locale est la même et que l’effort est identique.

Conclusion:
Si l’on regarde l’écart de contrainte uniquement sur la partie supérieure de l’œuf (zone dans laquelle la géométrie se différencie vraiment) on constate que la valeur est 4 fois moindre sur l’œuf.
La sphère en compression est donc beaucoup moins résistante que l’œuf.
Magique non ?
Un œuf est donc sacrément costaud et ceci est du uniquement à sa géométrie.
Bon, il ne faut pas oublier que la partie basse de l’œuf est aussi fragile que la sphère.
Tout ceci s’entend donc dans l’hypothèse où l’œuf est chargé intelligemment en prenant soin d’envelopper la partie basse et la pointe pour que le chargement soit le moins singulier possible.
On peut noter toutefois que la poule s’en fout complètement car elle couve son œuf sans se soucier de l’orientation de la charge. L’explication de sa résistance n’est donc pas dans l’utilisation qu’en fait la poule !
Dans cette mise en œuvre amusante d’un calcul sur Catia je vous ai montré comment préparer l’ensemble des modèles et comment introduire des contacts.
J’espère que cela vous a plu. Si c’est le cas, mettez un like et si vous avez des questions mettez les en dessous.
.
No responses yet