En RDM (Résistance des matériaux), le flambage (ou flambement) est un phénomène à absolument prendre en considération lorsque une partie d’une structure plutôt élancée est soumise à un effort de compression.

Vous l’avez certainement d’ailleurs déjà rencontré en poussant sur chaque extrémité d’une baguette de bois bien droite.
Celle-ci d’un seul coup se met à fléchir sous une charge pas si grande que cela.

Dans cet article, nous allons voir …
Comment évaluer le risque d’un flambage sur un barreau en compression avec Catia V5 ?
Pourquoi est-ce important d’un point de vue dimensionnement ?
Si l’on considère un petit bout de cylindre, disons aussi long que son diamètre, on s’apercevra en le chargeant en compression sur une machine qu’il est capable de résister à un effort de “compression pure” dépendant uniquement de sa matière.
En effet, ce solide s’écrasera plastiquement lorsque nous aurons dépassé la limite élastique.
Prenons maintenant un cylindre de même matière et de même section mais très allongé. En le chargeant progressivement de la même façon, on finit par transformer la compression initiale en flexion conduisant assez rapidement à la rupture de la pièce.
On a en fait activé une instabilité.
Ceci se produit à une charge bien plus faible que dans la compression du petit cylindre.
En considérant les conditions limites identiques, la limite de tenue ne dépend pas uniquement de la matière mais également de la forme (section et longueur).
En conception mécanique il est donc très important de se méfier de ce phénomène et de le prendre en compte lors du dimensionnement.
Considérer que la barre élancée ne voit qu’une contrainte en compression bien en deçà de la limite élastique s’expose à un gros risque.
Ce sera le cas pour les barres mais aussi les plaques, les coques… en compression.
Si les formules de RDM peuvent nous venir en aide pour des barres droites et à la limite des plaques, cela devient complexe pour des structures gauches ou ramifiées comme des châssis tubulaires ou des caissons.
Un logiciel de Calcul comme celui de Catia (GSA = Generative Structural Analysis) peut nous aider dans cette démarche.
Préparation du modèle.
Toute l’analyse du flambage part d’une analyse statique classique.
Il faut donc commencer par cela.
Dans cet exemple, nous allons voir le cas le plus à droite dans l’image de wikipédia (encastré-libre).
Le modèle Catpart est donc un simple cylindre solide (Corps de pièce principal).
C’est une barre en acier Ø32 mm, longueur 1000mm.

C’est ultra facile à ce niveau.
J’ai juste ajouté des paramètres utilisateur pour faire deux entrées:
- Le diamètre de la barre (mais je ne jouerai pas avec)
- La limite élastique du matériau (fixe aussi, totalement arbitraire mais réaliste)
et une sortie
- La section de la barre
Ces trois paramètres sont publiés (optionnel). Je les récupère dans la CataAnalysis.
Le modèle de calcul
Il est créé à partir du modèle précédent et donc en lien avec celui-ci.

On y trouve un maillage Octree (tétraèdres paraboliques taille 15mm) directement généré à partir du corps de pièce principal.
Le matériau est directement repris de la Catpart (un acier) et la propriété physique solide est automatiquement créée.
J’ai juste ajouté un encastrement sur une face plane d’extrémité et un chargement sur l’autre extrémité de façon à pousser sur la barre.
La valeur de la charge est pilotée par un paramètre visible en bas de l’image.
Cela permet de faire tourner le calcul et d’avoir un résultat rapidement.
Vous noterez que sur ce post-traitement (contraintes principales – minimum principales) on a une uniformité de la valeur (couleur) tout le long de la barre mais pas aux extrémités.
C’est du à la présence des conditions limites.
C’est un bon exemple pour illustrer le fait qu’il ne faut jamais chercher à post traiter (interpréter des valeurs) à ce niveau.
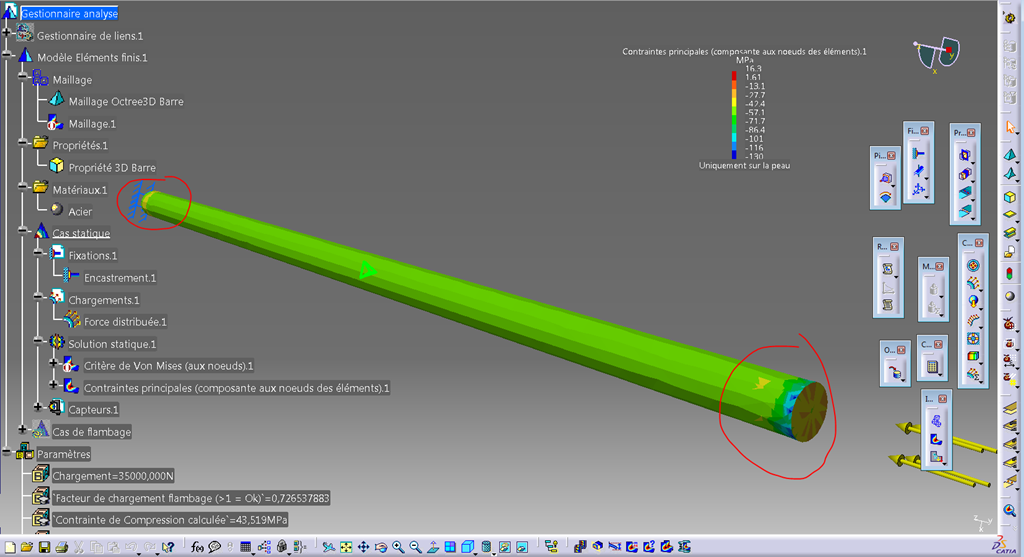
La valeur est constante en tous points de la barre

et correspond exactement à la valeur théorique.

que j’ai ressorti dans un paramètre utilisateur (en bas de l’image) avec cette formule:

Le paramètre “chargement” agit sur la force en bout de la barre et dans cette formule.
Le diviseur est ici le paramètre importé de la Catpart (“Surface section” publié).
De ce point de vue (compression pure), ça fonctionne et la barre est peu chargée.
43 Mpa en compression est bien inférieur à la limite élastique du matériau…
Oui mais !
Le Cas de Flambage
Sur Catia, un cas de flambage se crée à partir d’un cas statique.
Il suffit d’insérer un nouveau cas (donc de flambage) et de désigner la solution statique correspondante.
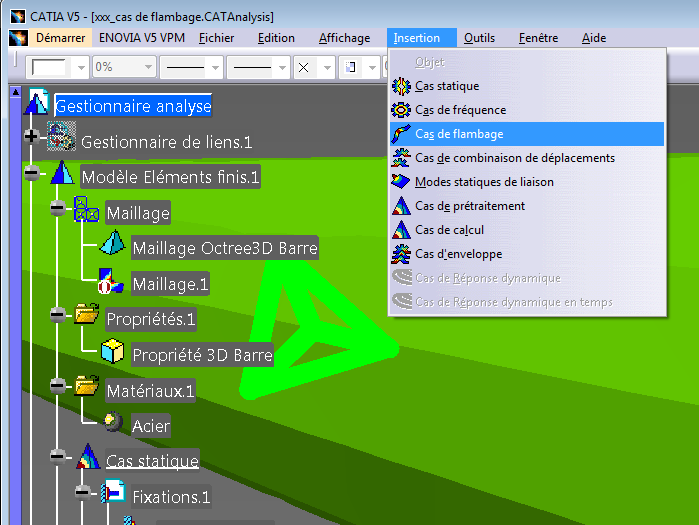
cela ajoute un nouveau cas et le rend courant.

En double cliquant sur “Solution de flambement”, on peut exiger un certain nombre de modes comme résultats de calcul
C’est quoi les modes ?
Cela correspond aux déformées potentielles de la pièce lorsqu’elle est soumise à une excitation.
Ici, l’excitation est un chargement statique mais cela pourrait aussi être une vibration.
Les modes de déformation sont numérotés par ordre croissant en fonction du nombre de nœuds (endroits où ça ne bouge pas) et de ventres (endroits où cela bouge le plus).
Il arrive comme ici que plusieurs modes soient équivalents car la pièce présente une ou plusieurs symétries.
On lance alors le calcul avec la petite calculatrice en demandant la résolution de tous les cas de calcul.
Sous “Solution de flambement” on a alors une image (si il n’y en a pas, un bouton droit / image / Maillage déformé).
”Maillage déformé” permet de visualiser les différents modes de flambage.
On a accès aux différents modes en double cliquant sur l’image et en allant dans l’onglet “Occurrences”.
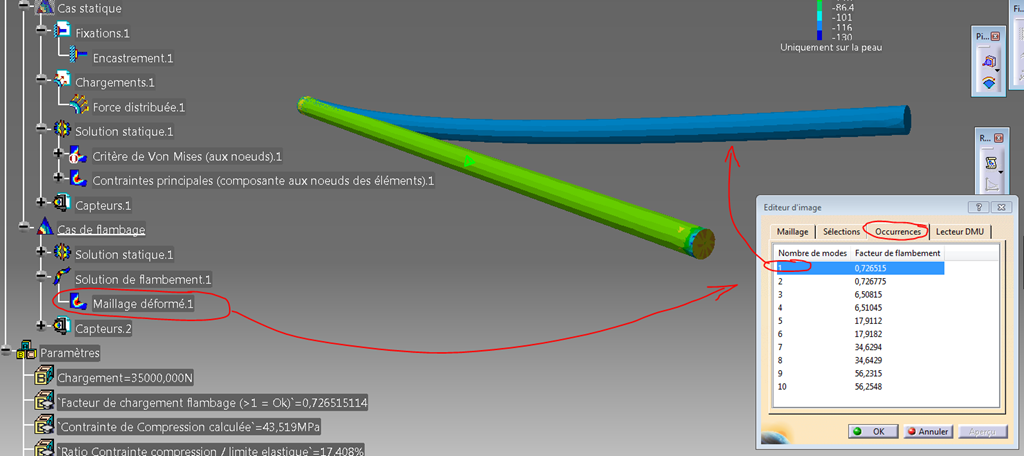
On voit ici que les modes 1 et 2, 3 et 4, 5 et 6, etc… ont deux à deux les même valeurs.
Ceci est dû à la symétrie de la pièce. Pour exemple, sur l’image précédente on a le premier mode et sur l’image ci-dessous le deuxième mode. En fait c’est la même chose mais tourné de 90°.
Il y a ici 10 modes extraits mais physiquement cela ne fait que 5 finalement.

Il y a ici un ventre (un grand déplacement à l’extrémité libre de la barre) et un nœud (pas de déplacement) à l’encastrement.
Regardons les modes 3 et 4:

Il y a un ventre (flèche) et deux nœuds (entourés)
Regardons les modes 5 et 6:

Il y a ici deux ventres (flèches) et 3 nœuds (entourés).
Vous remarquerez aussi que la valeur qui se trouve associée à ces modes sont identiques deux à deux.
Ces valeurs “facteur de flambement” nous donnent directement la réponse à la question du départ…
Avec cette charge, risque t’on d’activer un flambage ?
La question devrait être ici:
“Avec cette charge, risque t’on d’activer les modes de flambage 1 ou 2 ?”
La réponse ici est oui (image précédente) car la valeur est inférieure à 1.
Par contre, avec cette charge, on n’activera pas le deuxième vrai mode (modes 3 et 4 extraits) car le facteur de flambement et largement supérieur à 1.
En fait, en général pour activer le deuxième mode (ou plus), il faut passer par la charge critique du premier mode. On activera donc le premier mode et jamais le deuxième.
C’est du fait, assez difficile à obtenir ou alors il faut charger fortement et rapidement (un choc par exemple).
Je me suis amusé à chercher la valeur de charge critique minimale qui conduit au flambage de notre barre.
Je me suis servi d’un algorithme d’optimisation mais ce n’était pas nécessaire (voir plus loin).
La valeur trouvée est 25428 N.
On a alors un coefficient de flambement égal à 1.
- Si l’on diminue la charge on se retrouve dans un cas de compression pure et il ne se passe rien
- Si l’on maintient ou augmente la charge on a alors apparition de cette instabilité (flexion destructrice de la barre).
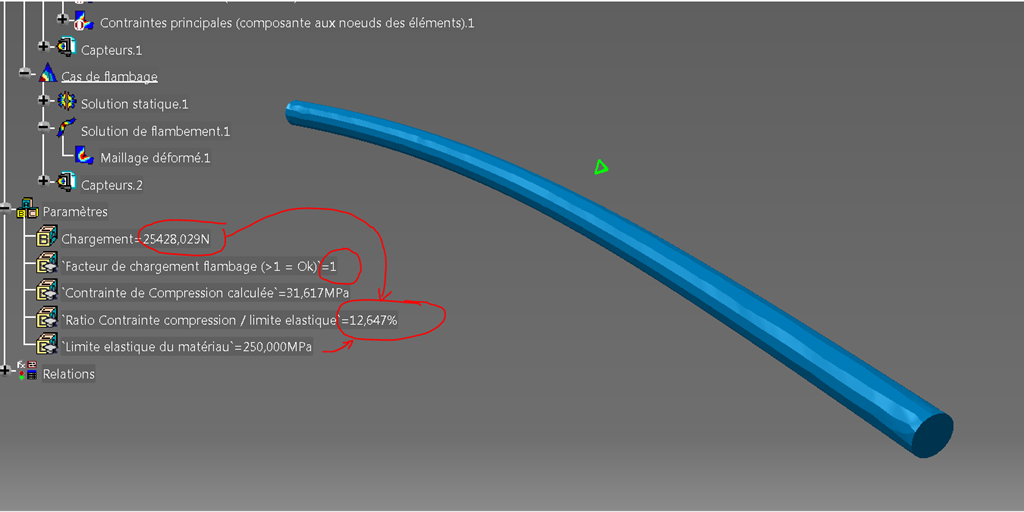
Le paramètre utilisateur de type “proportion” donne le ratio entre la contrainte en compression dans la barre et la limite élastique du matériau.
Que constate t’on ?
On voit que lorsque l’on atteint la charge (25428 N) critique (facteur=1) d’activation du premier mode de flambage , nous avons une contrainte de compression de 32 Mpa ce qui correspond à seulement 13% de la limite élastique du matériau !
Il est donc très dangereux de dimensionner une structure élancée et en compression uniquement sur un critère de limite en compression du matériau.
Le facteur de flambement permet de retrouver la charge critique en multipliant la charge appliquée par ce facteur.
Facteur <1 (surchargé = flambage)
Partant de la charge critique, si l’on augmente la charge, le facteur de flambement devient inférieur à 1 —> Il y a Flambage
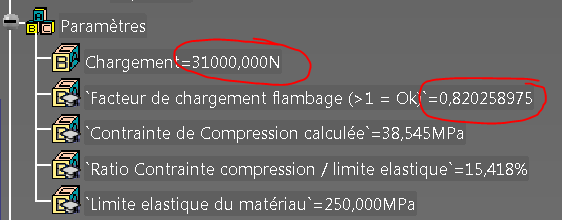
On a 31000 N et un facteur de 0.82 (<1 donc trop chargé).
31000×0.82=24420 N (valeur critique trouvée précédemment)
Facteur >1 (pas de flambage)
Partant de la charge critique, si l’on diminue la charge, le facteur de flambement devient supérieur à 1 —> Il y n’a théoriquement pas flambage.

On a 18000 N et un facteur de 1.4127 (>1).
18000×1.4127=24428 N (valeur critique trouvée précédemment)
Conclusion
Dans cet exemple, nous avons vu comment mettre en œuvre un calcul simple d’une barre ronde en compression afin de déterminer si sa charge peu ou non conduire à un flambage potentiel.
L’activation d’un telle instabilité dépend de la charge, du matériau, de la géométrie et également des conditions limites (la façon avec laquelle on maintient la pièce).
A travers ce simple exemple, on voit qu’il est assez facile d’atteindre le flambage d’un barre élancée et que la charge critique et la contrainte en compression associée sont très faibles en comparaison d’une tenue en compression pure.
Il convient donc de toujours rester attentif à ce phénomène lors d’une étude.
Derrière une compression peut se cacher un risque de flambage.
Les cas typiques sont les étagères, les ponts, les treillis tubulaires, les âmes de longeron, les cuves en dépression, les caissons de navires, les voilures d’avion…
Si ce genre d’article vous plaît et si vous en voulez d’autres dites le moi en commentaire ci-dessous
No responses yet